What Is Equivalent To 2/5
cibeltiagestion
Sep 07, 2025 · 6 min read
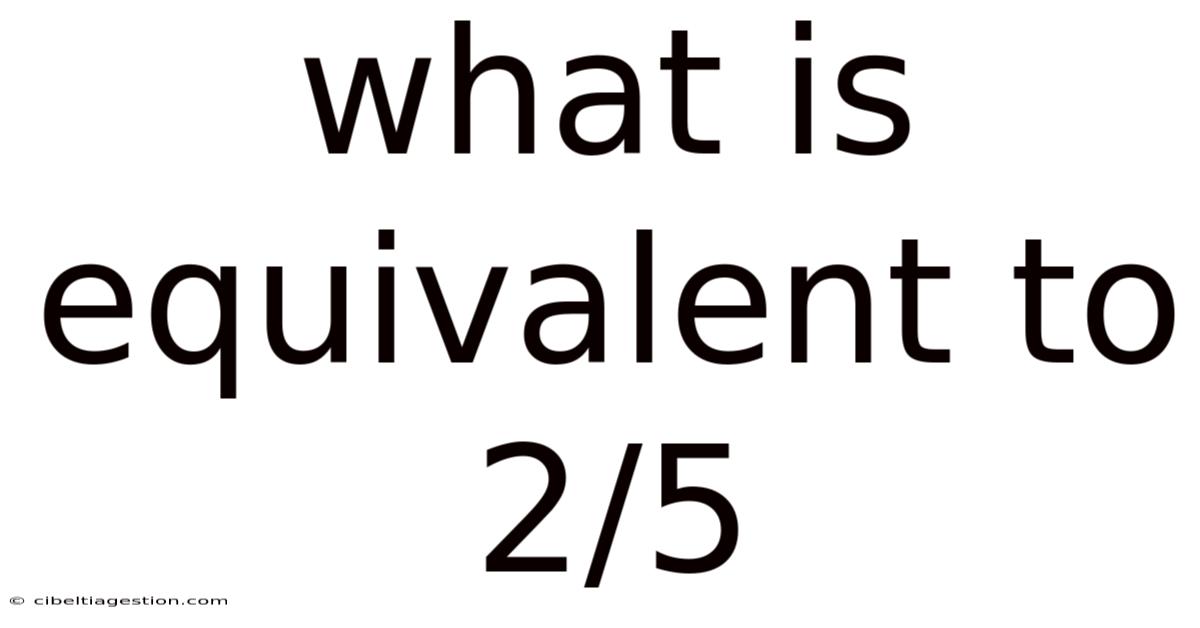
Table of Contents
Decoding Fractions: What is Equivalent to 2/5? A Comprehensive Guide
Understanding fractions is fundamental to mathematics and everyday life. This article delves deep into the concept of equivalent fractions, focusing specifically on finding fractions equivalent to 2/5. We'll explore various methods, explain the underlying principles, and provide practical examples to solidify your understanding. By the end, you'll not only know what's equivalent to 2/5 but also possess a robust understanding of fraction equivalence.
Understanding Fractions: A Quick Refresher
Before we dive into finding equivalents for 2/5, let's quickly revisit the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This means we have 2 parts out of a total of 5 equal parts.
What are Equivalent Fractions?
Equivalent fractions represent the same proportion or value, even though they look different. Imagine cutting a pizza into 5 slices and taking 2. Now imagine cutting the same pizza into 10 slices; you'd need to take 4 slices to have the same amount of pizza. Both 2/5 and 4/10 represent the same portion of the pizza – they are equivalent fractions.
Finding Equivalent Fractions to 2/5: The Core Methods
There are several reliable methods to find fractions equivalent to 2/5. Let's explore the most common and effective approaches:
1. Multiplying the Numerator and Denominator by the Same Number
This is the most straightforward method. To find an equivalent fraction, simply multiply both the numerator and the denominator of the original fraction (2/5) by the same non-zero number. This number can be any whole number.
- Example 1: Multiplying by 2: (2 x 2) / (5 x 2) = 4/10
- Example 2: Multiplying by 3: (2 x 3) / (5 x 3) = 6/15
- Example 3: Multiplying by 4: (2 x 4) / (5 x 4) = 8/20
- Example 4: Multiplying by 5: (2 x 5) / (5 x 5) = 10/25
- Example 5: Multiplying by 10: (2 x 10) / (5 x 10) = 20/50
As you can see, 4/10, 6/15, 8/20, 10/25, 20/50, and infinitely many other fractions are equivalent to 2/5. The key is to always multiply both the numerator and the denominator by the same number. This preserves the ratio and maintains the original value.
2. Dividing the Numerator and Denominator by their Greatest Common Divisor (GCD)
This method helps to simplify fractions to their lowest terms. The greatest common divisor (GCD) is the largest number that divides both the numerator and the denominator without leaving a remainder. If the GCD is 1, the fraction is already in its simplest form.
Let's illustrate this with an example: Consider the fraction 10/25. The GCD of 10 and 25 is 5. Dividing both the numerator and denominator by 5 gives us:
(10 ÷ 5) / (25 ÷ 5) = 2/5
This shows that 10/25 is equivalent to 2/5, and 2/5 is the simplest form of 10/25. Finding the GCD can sometimes require a bit of trial and error or the use of the Euclidean algorithm (a more advanced method for finding GCD).
3. Using Visual Representations
Visual aids can significantly improve understanding. Representing 2/5 visually, such as using a pie chart divided into 5 equal slices with 2 shaded, helps to grasp the concept. Creating similar visual representations for other fractions (like 4/10 or 6/15) will clearly show their equivalence.
Understanding the Principle Behind Equivalent Fractions
The fundamental principle behind equivalent fractions lies in the concept of proportion. Multiplying or dividing both the numerator and denominator by the same number doesn't change the ratio between them. The ratio remains constant, indicating that the fractions represent the same proportion or part of a whole.
Practical Applications of Equivalent Fractions
Equivalent fractions are essential in various mathematical operations and real-world scenarios:
- Simplifying fractions: Reducing a fraction to its simplest form makes calculations easier and provides a clearer understanding of the value.
- Adding and subtracting fractions: To perform these operations, fractions must have a common denominator. Finding equivalent fractions with a common denominator is crucial.
- Comparing fractions: Determining which fraction is larger or smaller becomes easier when comparing equivalent fractions with a common denominator.
- Real-world problems: Many real-world problems involving proportions, ratios, and percentages rely on the concept of equivalent fractions. For example, scaling recipes, calculating discounts, or understanding probabilities often involve finding equivalent fractions.
Frequently Asked Questions (FAQs)
Q1: Is there a limit to the number of equivalent fractions for 2/5?
A1: No, there are infinitely many equivalent fractions for 2/5. You can multiply the numerator and denominator by any non-zero whole number to generate a new equivalent fraction.
Q2: How do I know if two fractions are equivalent?
A2: Two fractions are equivalent if their simplest forms are identical. Alternatively, you can cross-multiply: if the product of the numerator of one fraction and the denominator of the other equals the product of the numerator of the second fraction and the denominator of the first, the fractions are equivalent. For example, for 2/5 and 4/10: (2 x 10) = (5 x 4) = 20.
Q3: What is the simplest form of a fraction?
A3: The simplest form of a fraction is when the numerator and denominator have no common factors other than 1 (their GCD is 1).
Q4: Why is it important to learn about equivalent fractions?
A4: Equivalent fractions are fundamental to a deeper understanding of fractions, ratios, proportions, and percentages. Mastering this concept is crucial for success in mathematics and many real-world applications.
Conclusion: Mastering the Equivalence of Fractions
This comprehensive guide has explored the concept of equivalent fractions, focusing specifically on finding fractions equivalent to 2/5. We've examined various methods, explained the underlying principles, and highlighted practical applications. Remember, the core principle is maintaining the ratio between the numerator and the denominator. By multiplying or dividing both by the same non-zero number, you create an equivalent fraction that represents the same proportion or value. Mastering this concept is crucial for building a strong foundation in mathematics and successfully tackling numerous mathematical challenges. Practice makes perfect, so continue working with different fractions to solidify your understanding of this essential mathematical concept. Through consistent practice and a thorough understanding of the underlying principles, you can confidently navigate the world of fractions and their equivalents.
Latest Posts
Latest Posts
-
3x 2 X 2 2
Sep 08, 2025
-
How Much Is Three Ounces
Sep 08, 2025
-
Is H2so3 Ionic Or Molecular
Sep 08, 2025
-
In Spain They Take Siestas
Sep 08, 2025
-
Aquaporins May Be Employed During
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is Equivalent To 2/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.