2 X 7 3x 12
cibeltiagestion
Sep 16, 2025 · 6 min read
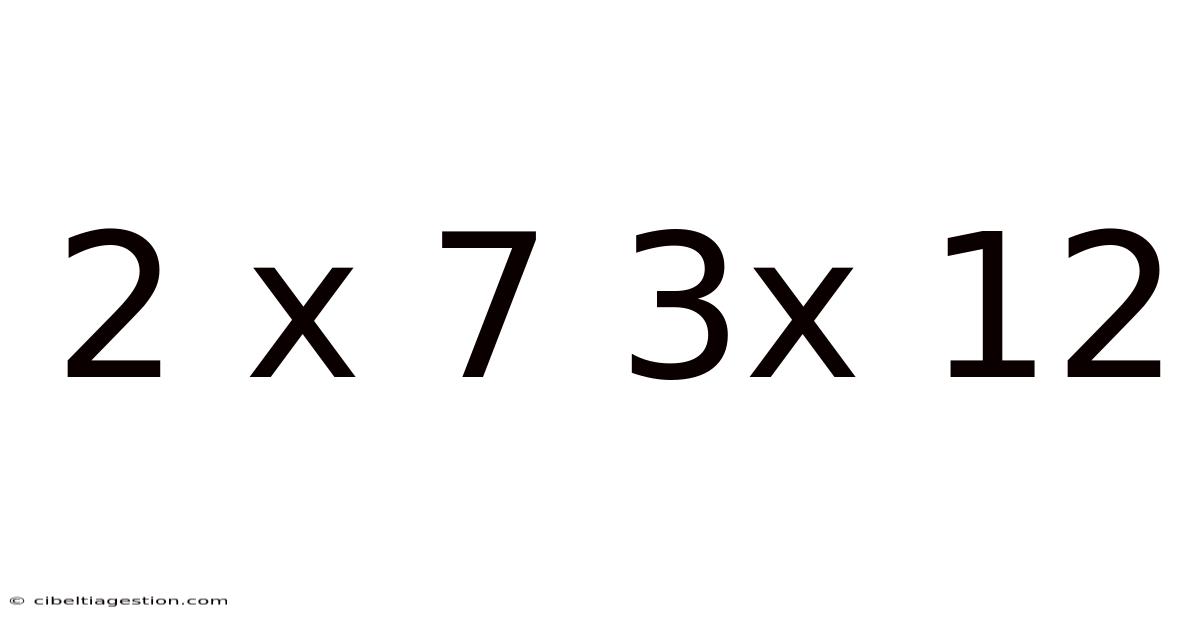
Table of Contents
Exploring the Mathematical Relationship: 2 x 7 and 3 x 12
This article delves into the seemingly simple mathematical expressions, 2 x 7 and 3 x 12, uncovering their underlying principles and exploring their applications within broader mathematical concepts. While the individual calculations are straightforward, examining them comparatively reveals valuable insights into multiplication, factors, multiples, and even the foundations of algebra. We will explore these expressions not just as isolated calculations, but as stepping stones to a deeper understanding of mathematical relationships.
Introduction: Beyond Simple Multiplication
At first glance, 2 x 7 = 14 and 3 x 12 = 36 seem like basic multiplication problems suitable for elementary school students. However, a closer look reveals a wealth of mathematical concepts hidden within these seemingly simple equations. This article aims to dissect these equations, exploring their factors, multiples, and the broader mathematical implications they represent. We’ll uncover the relationships between these numbers, discussing prime factorization, least common multiples (LCM), and greatest common divisors (GCD). This exploration will lay the groundwork for understanding more complex mathematical operations and concepts.
Understanding the Basics: Factors and Multiples
Before we delve deeper, let's establish a clear understanding of fundamental mathematical terms:
-
Factors: Factors are numbers that divide evenly into another number without leaving a remainder. For example, the factors of 14 are 1, 2, 7, and 14. Similarly, the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
-
Multiples: Multiples are the results of multiplying a number by any integer (whole number). For instance, multiples of 2 include 2, 4, 6, 8, 10, and so on. Multiples of 3 include 3, 6, 9, 12, 15, and so on. Notice that 6 is a multiple of both 2 and 3.
-
Prime Numbers: A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Prime numbers are the building blocks of all other numbers.
-
Composite Numbers: A composite number is a whole number greater than 1 that has more than two factors. Both 14 and 36 are composite numbers.
Prime Factorization: Deconstructing the Numbers
Prime factorization is the process of expressing a number as a product of its prime factors. This is a crucial concept in number theory and has numerous applications in more advanced mathematics. Let's apply it to our examples:
-
14 (2 x 7): This is already expressed as a product of its prime factors: 2 and 7. Both 2 and 7 are prime numbers.
-
36 (3 x 12): While this is a factorization, it's not a prime factorization. We need to break it down further. 12 is a composite number (2 x 2 x 3). Therefore, the prime factorization of 36 is 2 x 2 x 3 x 3, or 2² x 3².
Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Understanding the GCD and LCM is essential for simplifying fractions, solving equations, and working with rhythmic patterns in music.
-
Greatest Common Divisor (GCD): The GCD is the largest number that divides evenly into two or more numbers. Let's find the GCD of 14 and 36. The factors of 14 are 1, 2, 7, 14. The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36. The largest number that appears in both lists is 2. Therefore, the GCD of 14 and 36 is 2.
-
Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of two or more numbers. To find the LCM of 14 and 36, we can list their multiples or use their prime factorizations. The prime factorization of 14 is 2 x 7. The prime factorization of 36 is 2² x 3². To find the LCM, we take the highest power of each prime factor present in either factorization: 2² x 3² x 7 = 4 x 9 x 7 = 252. Therefore, the LCM of 14 and 36 is 252.
Applications in Real-World Scenarios
While these calculations might seem abstract, they have numerous practical applications:
-
Measurement and Conversions: Imagine you're tiling a floor. If each tile is 14 cm square, and the room is 36 cm wide, you need to use LCM to determine the smallest tile size to cover the entire area without needing to cut any tiles.
-
Scheduling: If one event occurs every 14 days and another every 36 days, the LCM tells you when both events will coincide again.
-
Music Theory: Understanding LCM is crucial in music theory when working with rhythmic patterns and finding common denominators for different time signatures.
Extending the Concept: Introduction to Algebra
The expressions 2 x 7 and 3 x 12 can serve as a springboard for understanding algebraic concepts. We can represent these equations using variables:
-
Let 'x' represent a number. Then 2x = 14 can be solved for x by dividing both sides by 2, giving x = 7.
-
Similarly, 3x = 36 can be solved for x by dividing both sides by 3, giving x = 12.
This simple demonstration shows how multiplication equations can be used to represent unknown quantities and how algebraic manipulation can be used to solve for those unknowns. This basic principle underpins much more complex algebraic problem-solving.
Exploring Further: Beyond the Basics
The exploration of 2 x 7 and 3 x 12 opens doors to numerous related mathematical areas:
-
Modular Arithmetic: The remainders when dividing by different numbers form the basis of modular arithmetic, which has applications in cryptography and computer science.
-
Number Patterns and Sequences: Studying the multiples of 14 and 36 reveals interesting patterns and sequences, offering insights into number theory.
-
Geometry and Area Calculations: These numbers could represent the dimensions of rectangles, leading to area calculations and explorations of geometric properties.
Frequently Asked Questions (FAQ)
Q: What is the difference between a factor and a multiple?
A: A factor divides evenly into a number, while a multiple is the result of multiplying a number by an integer. For example, 2 is a factor of 14, and 14 is a multiple of 2.
Q: Why is prime factorization important?
A: Prime factorization is fundamental to understanding number properties and is used extensively in various mathematical areas, including cryptography and simplifying fractions.
Q: How can I calculate the GCD and LCM efficiently for larger numbers?
A: The Euclidean algorithm is an efficient method for calculating the GCD of two numbers. For the LCM, once the GCD is known, the LCM can be calculated using the formula: LCM(a, b) = (a x b) / GCD(a, b).
Q: What are some real-world applications of LCM and GCD?
A: LCM is useful in scheduling and in situations where you need to find a common denominator (like in music theory). GCD is helpful in simplifying fractions and in certain types of measurement problems.
Conclusion: A Foundation for Further Exploration
While seemingly simple, the mathematical expressions 2 x 7 and 3 x 12 provide a gateway to understanding fundamental mathematical concepts like factors, multiples, prime factorization, GCD, and LCM. These concepts are not merely abstract ideas; they have practical applications in various fields, from scheduling and measurement to music and cryptography. By exploring these seemingly simple equations, we've laid a solid foundation for understanding more complex mathematical principles and problem-solving strategies. The journey of mathematical understanding is a continuous one, and these basic equations serve as crucial stepping stones on that path. Further exploration of these concepts will inevitably lead to a deeper appreciation of the elegance and power of mathematics.
Latest Posts
Latest Posts
-
12 Out Of 16 Percentage
Sep 16, 2025
-
Energy Diagram For Exothermic Reaction
Sep 16, 2025
-
Cm 2 To M 2
Sep 16, 2025
-
Factor X 2 6x 9
Sep 16, 2025
-
Convert 55 C To F
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2 X 7 3x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.