6 X 3 X 3
cibeltiagestion
Sep 15, 2025 · 7 min read
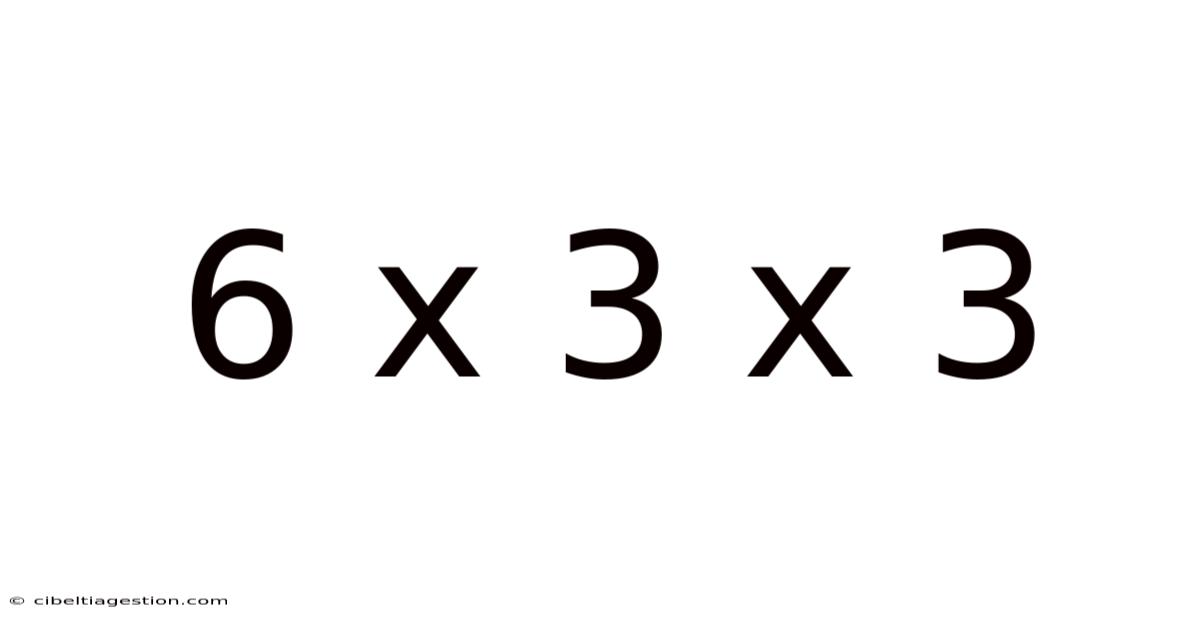
Table of Contents
Decoding 6 x 3 x 3: Exploring Dimensions, Applications, and Beyond
This article delves into the seemingly simple mathematical expression "6 x 3 x 3," uncovering its multifaceted meanings and applications across various fields. While seemingly straightforward, this expression offers a gateway to understanding fundamental concepts in mathematics, geometry, and even problem-solving strategies. We'll explore its numerical value, geometrical interpretations, practical applications, and delve into related mathematical concepts to provide a comprehensive understanding.
I. The Fundamental Calculation: 6 x 3 x 3 = ?
The core of "6 x 3 x 3" lies in its straightforward mathematical computation. Following the order of operations (multiplication from left to right), we get:
6 x 3 = 18
18 x 3 = 54
Therefore, 6 x 3 x 3 = 54. This seemingly simple calculation forms the foundation for understanding more complex applications and interpretations.
II. Geometrical Interpretations: Visualizing 6 x 3 x 3
The expression "6 x 3 x 3" can be readily visualized in three-dimensional space. Imagine a rectangular prism (also known as a cuboid). The numbers represent the dimensions of this prism:
- 6: Represents the length of the prism.
- 3: Represents the width of the prism.
- 3: Represents the height of the prism.
Therefore, "6 x 3 x 3" can be interpreted as the calculation of the volume of this rectangular prism. The volume is obtained by multiplying its length, width, and height, resulting in 54 cubic units. This geometrical interpretation provides a tangible representation of the numerical value.
We can further explore this geometrical visualization. Consider different arrangements of these dimensions. While the volume remains 54 cubic units, the shape of the rectangular prism changes depending on which number represents length, width, or height. This highlights how the same numerical value can represent different physical configurations.
III. Applications in Real-World Scenarios
The concept of "6 x 3 x 3," or more broadly, the calculation of volumes, has numerous practical applications across various fields:
-
Construction and Engineering: Calculating the volume of materials required for building projects, like concrete for a foundation or bricks for a wall. Understanding cubic measurements is crucial for accurate material estimations and cost calculations. A contractor might need to order enough concrete to fill a foundation with dimensions similar to our 6 x 3 x 3 prism.
-
Packaging and Shipping: Determining the cubic volume of packages is vital for shipping and logistics. Companies optimize package sizes to minimize shipping costs and maximize space utilization within containers or trucks. A company shipping small boxes might use the dimensions 6 x 3 x 3 inches to calculate the volume of each box and determine the most efficient packaging arrangements.
-
Agriculture and Farming: Calculating the volume of soil required for planting, or the capacity of storage containers for harvested crops. Farmers often deal with large quantities of materials, so accurate volume calculations are essential for planning and management. A farmer might use the dimensions 6 x 3 x 3 meters to calculate the volume of a storage silo for grain.
-
Aquariums and Fish Tanks: The volume of water in an aquarium is calculated using similar principles. Understanding volume allows for accurate estimations of the amount of water needed and the number of fish that can be safely housed.
-
Medicine and Pharmaceuticals: Calculating dosages and volumes of medications is crucial in pharmaceutical applications. Precise measurements are critical for ensuring the safety and effectiveness of treatments.
IV. Expanding the Concept: Beyond Simple Multiplication
While "6 x 3 x 3" is a simple calculation, it opens doors to understanding more complex mathematical concepts. Let's explore some related ideas:
-
Factors and Multiples: The numbers 6, 3, and 3 are factors of 54. Understanding factors and multiples is fundamental to number theory and algebra. We can analyze the prime factorization of 54 (2 x 3 x 3 x 3) to gain deeper insights into its numerical properties.
-
Cubic Units and Volume: The result of 54 represents cubic units, a fundamental unit of volume. Understanding cubic measurements is essential in various scientific and engineering disciplines. We could extend this concept to explore different units of volume, such as cubic centimeters, cubic meters, or even cubic feet, depending on the scale of the problem.
-
Surface Area: While we focused on volume, calculating the surface area of our 6 x 3 x 3 prism is another related geometrical concept. The surface area is the sum of the areas of all the faces of the prism. This involves more complex calculations, but it's a valuable extension of the initial problem.
-
Three-Dimensional Geometry: The concept of "6 x 3 x 3" extends into the broader field of three-dimensional geometry. This involves studying shapes and objects in three-dimensional space, their properties, and their relationships. This opens up the study of more complex shapes like spheres, cylinders, and cones, whose volume calculations involve different formulas.
-
Algebraic Representation: We could represent the volume calculation algebraically. Let 'l' represent length, 'w' represent width, and 'h' represent height. The volume (V) can be expressed as: V = l x w x h. This algebraic representation allows us to generalize the calculation to any rectangular prism with known dimensions.
V. Problem-Solving and Critical Thinking
The seemingly simple calculation "6 x 3 x 3" serves as an excellent starting point for developing problem-solving skills. It encourages us to think critically and apply our knowledge to real-world scenarios. Consider these examples:
-
Scenario 1: A rectangular box needs to hold exactly 54 cubic centimeters of sand. What are some possible dimensions for the box? This problem encourages exploration of different combinations of factors that multiply to 54.
-
Scenario 2: A builder is constructing a small storage shed. They have enough materials to build a shed with a volume of 54 cubic meters. What are some possible dimensions for the shed? This problem extends the concept to real-world constraints and material limitations.
-
Scenario 3: A company is designing a new box for a product. They want the box to have a volume of 54 cubic inches but minimize the amount of cardboard used. This problem introduces optimization, a critical aspect of many engineering and design problems. Finding the dimensions that minimize surface area while maintaining a specific volume is a more challenging problem.
VI. Frequently Asked Questions (FAQ)
Q: What is the only prime number that is even?
A: 2 is the only even prime number. All other even numbers are divisible by 2 and therefore not prime.
Q: What is the difference between a rectangular prism and a cube?
A: A cube is a special type of rectangular prism where all sides (length, width, and height) are equal. A rectangular prism has three dimensions, but they don't have to be the same length.
Q: How can I calculate the surface area of a 6 x 3 x 3 rectangular prism?
A: To calculate the surface area, find the area of each face and add them together. There are two faces with dimensions 6 x 3, two with 6 x 3, and two with 3 x 3. The surface area would be 2(6 x 3) + 2(6 x 3) + 2(3 x 3) = 72 square units.
Q: Are there other ways to visualize 6 x 3 x 3 besides a rectangular prism?
A: While a rectangular prism is the most straightforward visualization, you could conceptually arrange 54 individual units into various three-dimensional arrays, though the rectangular prism offers the most efficient and easily calculable arrangement.
VII. Conclusion: A Simple Calculation, Profound Implications
The seemingly simple expression "6 x 3 x 3" offers a gateway to understanding fundamental mathematical concepts, geometrical principles, and problem-solving strategies. From calculating volumes of real-world objects to exploring factors and multiples, this expression demonstrates the interconnectedness of various mathematical fields. By understanding this simple calculation and its applications, we gain a deeper appreciation for the power and relevance of mathematics in everyday life. Furthermore, the exploration of this expression encourages critical thinking, problem-solving skills, and the ability to visualize abstract concepts in tangible ways. The simplicity of the starting point allows for complex explorations and applications, highlighting the vast possibilities that lie within even the most basic mathematical operations.
Latest Posts
Latest Posts
-
111 12 9
Sep 15, 2025
-
The Weimar Government Collapsed In
Sep 15, 2025
-
What Is A Genre Painting
Sep 15, 2025
-
Make Sure That Your Pet
Sep 15, 2025
-
What Times What Equals 20
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 6 X 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.