Factor 2x 2 7x 3
cibeltiagestion
Sep 10, 2025 · 5 min read
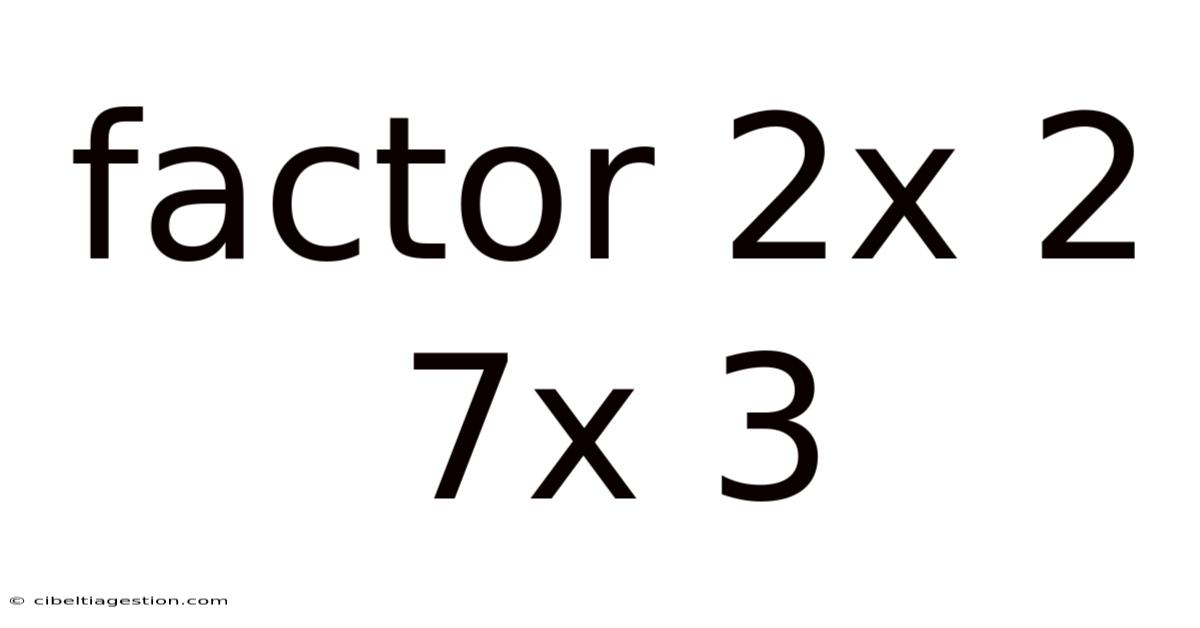
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 2x² + 7x + 3
This article provides a comprehensive guide to factoring the quadratic expression 2x² + 7x + 3. We'll explore various methods, delve into the underlying mathematical principles, and address common student questions. Understanding quadratic factoring is crucial for advanced algebra, calculus, and numerous applications in science and engineering. By the end, you'll not only be able to factor this specific expression but also master the techniques to tackle similar problems confidently.
Introduction: Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It takes the general form ax² + bx + c, where a, b, and c are constants, and 'a' is not equal to zero. Factoring a quadratic expression means rewriting it as a product of two simpler expressions, usually two binomials. This process is fundamental in solving quadratic equations and simplifying complex algebraic expressions. Our focus here is on factoring the specific quadratic 2x² + 7x + 3.
Method 1: The AC Method (Factoring by Grouping)
This method is particularly useful for factoring quadratic expressions where the coefficient of x² (the 'a' term) is not 1. Here's how it works for 2x² + 7x + 3:
-
Find the product 'ac': In our expression, a = 2 and c = 3, so ac = 2 * 3 = 6.
-
Find two numbers that add up to 'b' and multiply to 'ac': We need two numbers that add up to 7 (our 'b' term) and multiply to 6. These numbers are 6 and 1 (6 + 1 = 7 and 6 * 1 = 6).
-
Rewrite the middle term: Replace the '7x' term with '6x + 1x': 2x² + 6x + 1x + 3
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- 2x(x + 3) + 1(x + 3)
-
Factor out the common binomial: Notice that both terms now share the binomial '(x + 3)'. Factor this out:
- (x + 3)(2x + 1)
Therefore, the factored form of 2x² + 7x + 3 is (x + 3)(2x + 1).
Method 2: Trial and Error
This method involves a bit of guesswork, but it can be quicker once you get the hang of it. It relies on understanding how binomials multiply to form a quadratic expression.
-
Consider the factors of the 'a' term: The coefficient of x² is 2, which has factors of 1 and 2. These will be the coefficients of 'x' in our binomials.
-
Consider the factors of the 'c' term: The constant term is 3, which has factors of 1 and 3. These will be the constant terms in our binomials.
-
Test different combinations: We need to find the combination that results in the correct middle term (7x). Let's try some possibilities:
- (x + 1)(2x + 3): Expanding this gives 2x² + 5x + 3 (incorrect)
- (x + 3)(2x + 1): Expanding this gives 2x² + 7x + 3 (correct!)
Therefore, using trial and error, we arrive at the same factored form: (x + 3)(2x + 1).
Method 3: Using the Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can help find the roots (solutions) of the quadratic equation 2x² + 7x + 3 = 0. These roots can then be used to determine the factors.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
For our equation, a = 2, b = 7, and c = 3. Plugging these values into the formula:
x = [-7 ± √(7² - 4 * 2 * 3)] / (2 * 2) x = [-7 ± √(49 - 24)] / 4 x = [-7 ± √25] / 4 x = (-7 ± 5) / 4
This gives us two solutions:
- x = (-7 + 5) / 4 = -1/2
- x = (-7 - 5) / 4 = -3
These roots correspond to the factors (x + 3) and (2x + 1). Remember that if a root is 'r', then (x - r) is a factor. Thus, x = -3 implies (x + 3) and x = -1/2 implies (2x + 1).
Explanation of the Mathematical Principles
The methods above rely on the distributive property of multiplication (also known as the FOIL method: First, Outer, Inner, Last). When you expand (x + 3)(2x + 1), you get:
- First: x * 2x = 2x²
- Outer: x * 1 = x
- Inner: 3 * 2x = 6x
- Last: 3 * 1 = 3
Combining these terms gives 2x² + x + 6x + 3 = 2x² + 7x + 3. This demonstrates how the factored form expands to the original quadratic expression.
Frequently Asked Questions (FAQ)
-
What if the quadratic expression can't be factored easily? Not all quadratic expressions can be factored neatly using integers. In such cases, you might need to use the quadratic formula to find the roots and express the factors in a more complex form. Or, you could leave the expression in its original form.
-
Why is factoring important? Factoring simplifies expressions, making them easier to manipulate and solve equations. It's essential for solving quadratic equations, simplifying rational expressions, and in many applications of mathematics beyond algebra.
-
Can I use a calculator or software to factor quadratics? Yes, many calculators and online tools can factor quadratic expressions. However, understanding the methods manually is crucial for developing a deeper understanding of the underlying mathematical concepts.
-
What are some common mistakes students make when factoring? Common errors include incorrect signs, forgetting to check the middle term after expanding, and not considering all possible factor combinations. Careful attention to detail is essential.
Conclusion: Mastering Quadratic Factoring
Factoring quadratic expressions like 2x² + 7x + 3 is a fundamental skill in algebra. We’ve explored three different methods—the AC method, trial and error, and an indirect approach using the quadratic formula—all leading to the same result: (x + 3)(2x + 1). Mastering these techniques will not only help you solve specific problems but also build a strong foundation for more advanced mathematical concepts. Remember to practice regularly and thoroughly check your work to avoid common errors. With consistent effort, you’ll become proficient in factoring quadratic expressions and confident in your algebraic skills. The key is understanding the underlying principles and choosing the method that best suits your learning style and the specific problem at hand.
Latest Posts
Latest Posts
-
Is Hexane Polar Or Nonpolar
Sep 10, 2025
-
Un Automovilista Debe Saber Que
Sep 10, 2025
-
Square Root Of 20 Simplified
Sep 10, 2025
-
Honest Is To Genuine As
Sep 10, 2025
-
Slider Owns A Hamburger Restaurant
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 7x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.