Square Root Of 20 Simplified
cibeltiagestion
Sep 10, 2025 · 5 min read
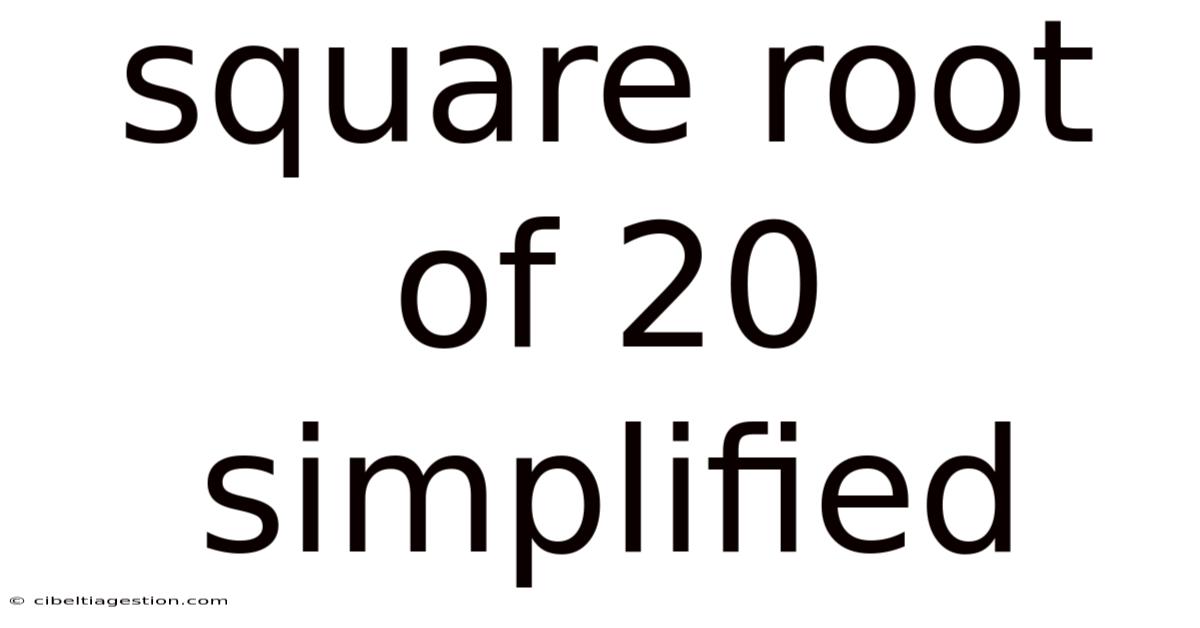
Table of Contents
Unveiling the Mystery: Simplifying the Square Root of 20
The square root of 20, often written as √20, might seem like a simple mathematical expression. However, understanding how to simplify it reveals fundamental concepts in algebra and number theory, offering a deeper appreciation for the beauty and logic within mathematics. This article will guide you through the process of simplifying √20, exploring the underlying principles, and answering frequently asked questions. We'll go beyond a simple answer, delving into the why and how, ensuring a comprehensive understanding for learners of all levels.
Understanding Square Roots and Simplification
Before diving into the simplification of √20, let's establish a solid foundation. A square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Not all numbers have perfect square roots (integers). Numbers like 20, for instance, don't have a whole number as their square root. This is where simplification comes in. Simplifying a square root means expressing it in its simplest radical form, removing any perfect square factors from within the radical sign.
Step-by-Step Simplification of √20
Simplifying √20 relies on the property of square roots that allows us to break down a number into its prime factors. Here's a step-by-step guide:
-
Find the Prime Factorization: The first step is to find the prime factorization of 20. Prime factorization is expressing a number as a product of its prime numbers (numbers only divisible by 1 and themselves). The prime factorization of 20 is 2 x 2 x 5, or 2² x 5.
-
Rewrite the Square Root: Now rewrite √20 using the prime factorization: √(2² x 5).
-
Apply the Product Rule of Radicals: The product rule states that √(a x b) = √a x √b. Applying this rule, we get: √2² x √5.
-
Simplify the Perfect Square: We know that √2² is simply 2 (because 2 x 2 = 4, and √4 =2). Therefore, our expression becomes: 2√5.
-
Final Simplified Form: The simplified form of √20 is 2√5. This means that 2√5 multiplied by itself equals 20.
The Mathematical Justification: A Deeper Dive
The simplification process is underpinned by fundamental mathematical properties. Let's explore the underlying principles in more detail:
-
Prime Factorization: Breaking down a number into its prime factors is crucial because it allows us to identify perfect squares hidden within the number. Perfect squares, like 4 (2²), 9 (3²), and 16 (4²), are easily extracted from the radical sign.
-
Product Rule of Radicals: This rule is a direct consequence of the definition of a square root. Since √a represents a number that, when multiplied by itself, equals a, and similarly for √b, then their product, √a x √b, when squared, results in a x b. This justifies the ability to separate the radical into individual factors.
-
Power Rules of Exponents: The simplification process also involves the understanding of exponent rules. When we have √2², this is equivalent to (2²)^(1/2). Using the power rule of exponents, (aᵐ)ⁿ = a^(m x n), we get 2^(2 x (1/2)) = 2¹. This reinforces why √2² simplifies to 2.
Practical Applications and Real-World Examples
Simplifying square roots isn't just an abstract mathematical exercise. It has practical applications across various fields:
-
Geometry: Calculating the diagonal of a square or rectangle often involves square roots. Simplifying these roots helps in precise measurements and calculations.
-
Physics: Many physics equations involve square roots, particularly in problems related to velocity, acceleration, and energy. Simplifying radicals allows for cleaner and more efficient calculations.
-
Engineering: Similar to physics, engineering relies heavily on mathematical calculations, and simplifying square roots contributes to accuracy and efficiency in designs and structural analysis.
-
Computer Graphics: In computer graphics and game development, square roots are used extensively in calculations involving distances, vectors, and rotations. Simplifying radicals improves performance and efficiency.
Frequently Asked Questions (FAQ)
Q1: Can all square roots be simplified?
A1: No. Square roots of perfect squares (like √9 = 3) are already in their simplest form. However, most square roots of non-perfect squares can be simplified by extracting perfect square factors.
Q2: What if the number inside the square root is negative?
A2: The square root of a negative number involves imaginary numbers, represented by the symbol 'i', where i² = -1. For example, √-4 = 2i. Simplifying these involves similar principles but incorporates imaginary units.
Q3: Are there other methods to simplify square roots?
A3: While the prime factorization method is the most common and widely applicable, other approaches might be employed depending on the number's characteristics. However, the underlying principle of identifying and extracting perfect square factors remains consistent.
Q4: What if I make a mistake in the prime factorization step?
A4: An incorrect prime factorization will lead to an inaccurate simplification. Carefully check each step to ensure all factors are prime. You can verify your prime factorization by multiplying the factors together to confirm you get the original number.
Q5: How can I improve my skills in simplifying square roots?
A5: Consistent practice is key. Start with simple numbers and gradually work towards more complex ones. Understanding prime factorization and exponent rules is crucial. Regularly reviewing the steps and working through various examples will build your proficiency.
Conclusion
Simplifying √20 to 2√5 is more than just a mathematical procedure; it's a journey into the fundamental principles of algebra and number theory. By understanding the underlying concepts of prime factorization, the product rule of radicals, and exponent rules, we can confidently tackle more complex radical expressions. The ability to simplify square roots is a valuable skill applicable to various fields, showcasing the practical relevance of seemingly abstract mathematical concepts. Remember, the key is to break down the problem into manageable steps, ensuring a thorough understanding of each stage. With consistent practice, simplifying square roots becomes second nature, revealing the inherent elegance and logic at the heart of mathematics.
Latest Posts
Latest Posts
-
Love Is A Bad Name
Sep 10, 2025
-
2 8 8 Organizing Class Roster
Sep 10, 2025
-
Where Is The Church Located
Sep 10, 2025
-
Effective Nuclear Charge Of Silicon
Sep 10, 2025
-
What Plus What Equals 24
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 20 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.