What Plus What Equals 24
cibeltiagestion
Sep 10, 2025 · 5 min read
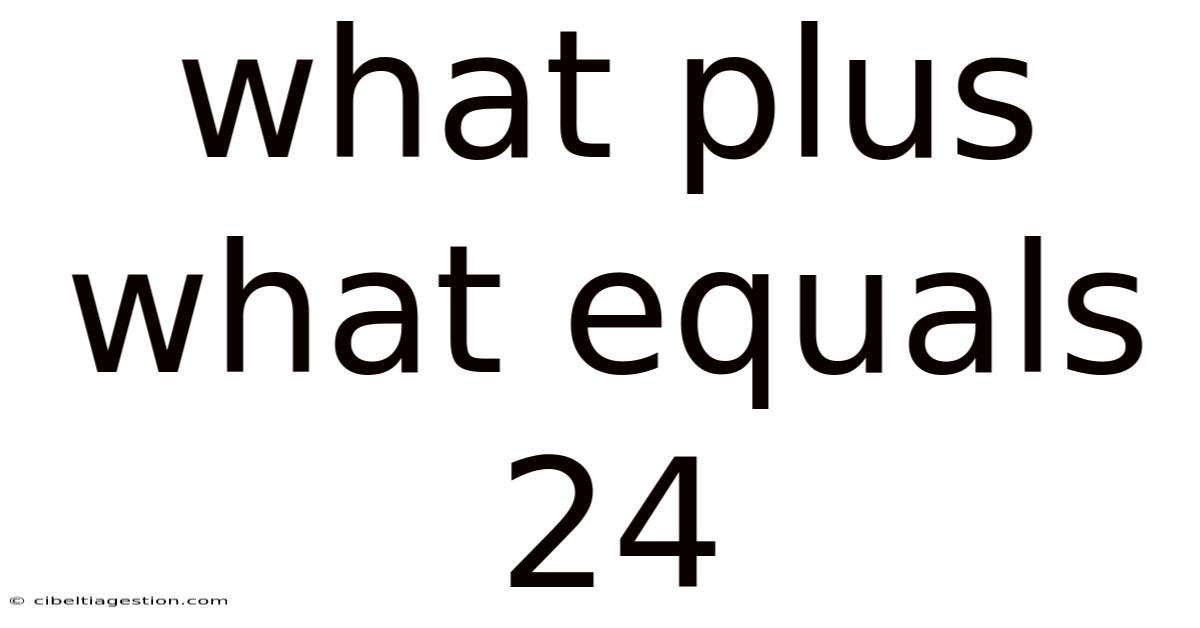
Table of Contents
What Plus What Equals 24? Exploring the Possibilities of Addition
This seemingly simple question, "What plus what equals 24?", opens a fascinating world of mathematical exploration. It's a gateway to understanding number relationships, different approaches to problem-solving, and even delving into more advanced mathematical concepts. This article will explore various ways to arrive at the answer, examining whole numbers, fractions, decimals, and even negative numbers, thereby demonstrating the versatility of addition. We'll delve into the practical applications of this seemingly basic arithmetic operation and dispel any misconceptions about finding solutions. This comprehensive guide is perfect for anyone looking to improve their understanding of addition and its broader mathematical implications.
Understanding the Basics of Addition
At its core, addition is the process of combining two or more numbers to find their total, or sum. In the context of "what plus what equals 24," we're looking for two addends (the numbers being added) that result in a sum of 24. The simplest approach is to think of whole numbers. Let's start there.
Whole Number Combinations that Equal 24
There are numerous combinations of whole numbers that add up to 24. Here are a few examples:
- 12 + 12 = 24
- 11 + 13 = 24
- 10 + 14 = 24
- 9 + 15 = 24
- 8 + 16 = 24
- 7 + 17 = 24
- 6 + 18 = 24
- 5 + 19 = 24
- 4 + 20 = 24
- 3 + 21 = 24
- 2 + 22 = 24
- 1 + 23 = 24
- 0 + 24 = 24
This list demonstrates that there isn't one single "correct" answer. The beauty of this problem lies in its multiplicity of solutions. This highlights the commutative property of addition, meaning that the order of the addends doesn't affect the sum (e.g., 10 + 14 is the same as 14 + 10).
Expanding Beyond Whole Numbers: Fractions and Decimals
The possibilities expand exponentially when we consider fractions and decimals. For example:
- 12.5 + 11.5 = 24
- 10.75 + 13.25 = 24
- 23.5 + 0.5 = 24
- 1/2 + 47/2 = 24 (This converts to 0.5 + 23.5 = 24)
- 1/4 + 95/4 = 24 (This converts to 0.25 + 23.75 = 24)
These examples showcase that the number of possible combinations becomes virtually limitless when we incorporate fractions and decimals. The key is to understand that any two numbers whose sum is 24 are valid solutions.
Introducing Negative Numbers
Adding a layer of complexity, we can introduce negative numbers into the equation. Remember that adding a negative number is the same as subtracting a positive number. Here's how this works:
- 30 + (-6) = 24
- 25 + (-1) = 24
- 26 + (-2) = 24
- 100 + (-76) = 24
This expands the possibilities even further. We can find pairs of numbers, one positive and one negative, that add up to 24. This demonstrates the flexibility and broad application of addition.
Practical Applications and Real-World Examples
The seemingly simple equation, "what plus what equals 24," has numerous practical applications in various fields. Consider these examples:
- Inventory Management: A store owner might need to determine how many more units of a product to order if they have 10 units in stock and need a total of 24. The answer, found by solving 10 + x = 24, is 14.
- Finance: Someone budgeting might allocate $10 for groceries and $14 for entertainment, totaling $24 for their daily spending.
- Construction: A builder measuring the length of a wall might need to add two sections together: a 12-foot section and a 12-foot section, resulting in a total length of 24 feet.
- Baking: A baker might use 12 ounces of flour in one recipe and 12 ounces in another, requiring a total of 24 ounces of flour.
These examples showcase how addition, and the problem of finding two numbers that sum to 24, is applicable in everyday situations, highlighting the practical importance of basic arithmetic.
Algebraic Approach to Finding Solutions
We can use algebra to formally represent the problem. Let's use 'x' and 'y' to represent the two unknown numbers:
x + y = 24
To solve for x and y, we need another equation, or a constraint. Without a constraint, there are infinite solutions. For example, if we let x = 1, then y = 23. If we let x = 10, then y = 14, and so on.
If we introduce a constraint, such as "x must be greater than y", we limit the number of solutions. However, even with constraints, we will still have multiple solutions unless we introduce further restrictions.
Addressing Common Misconceptions
A common misconception about addition problems like this is the belief that there's only one "right" answer. As demonstrated throughout this article, there are countless solutions. The key is understanding that addition is a flexible operation with a broad range of applications. Another misconception is the assumption that only whole numbers can be used. This is untrue; fractions, decimals, and negative numbers are all valid options.
Conclusion: The Richness of a Simple Equation
The seemingly simple question, "What plus what equals 24?", has led us on a journey through various mathematical concepts and real-world applications. From whole numbers to fractions, decimals, and negative numbers, the number of possible solutions is vast. This exploration underscores the importance of understanding the fundamental principles of addition and its versatility in problem-solving across numerous disciplines. The richness of this simple equation highlights the beauty and power of mathematics in its ability to explain and solve problems in our daily lives. It’s not simply about finding the answer; it’s about exploring the methods, understanding the concepts, and appreciating the diverse solutions that exist. Remember, there are many paths to 24!
Latest Posts
Latest Posts
-
What Do Blood Taste Like
Sep 10, 2025
-
Wingdings Font Character Code 110
Sep 10, 2025
-
1 8 Divided 3 4
Sep 10, 2025
-
4 5 Million Yen To Usd
Sep 10, 2025
-
5 2 Independent Practice Answer Key
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Plus What Equals 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.