Simplify 3x 2 3x 2
cibeltiagestion
Sep 14, 2025 · 5 min read
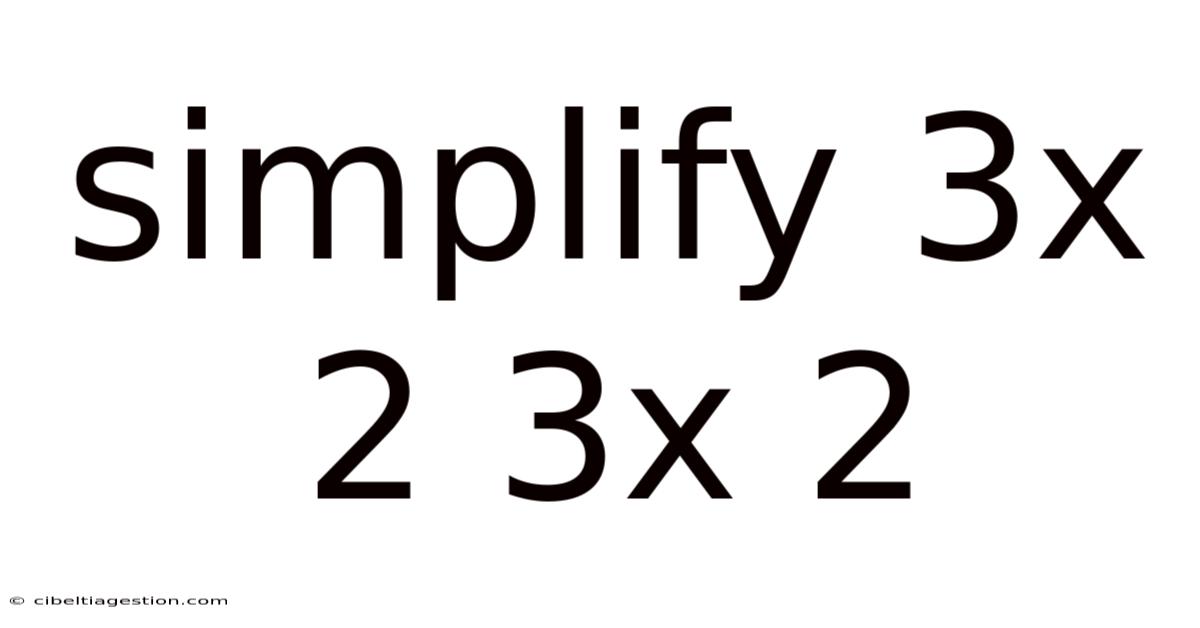
Table of Contents
Simplifying 3x² + 3x²: A Comprehensive Guide to Algebraic Expressions
This article provides a comprehensive guide to simplifying the algebraic expression 3x² + 3x². We will explore the fundamental concepts of algebra, specifically focusing on combining like terms, and demonstrate the process step-by-step. Understanding this seemingly simple problem forms the basis for tackling more complex algebraic manipulations later on. This guide is designed for students of all levels, from beginners grasping basic algebraic concepts to those seeking a refresher on fundamental principles. We will also delve into the underlying mathematical principles and address frequently asked questions.
Understanding Algebraic Expressions
Before we dive into simplifying 3x² + 3x², let's establish a clear understanding of what constitutes an algebraic expression. An algebraic expression is a mathematical phrase that combines numbers, variables, and operators (+, -, ×, ÷). Variables, usually represented by letters like x, y, or z, represent unknown quantities. In our example, x is the variable. The number in front of the variable is called the coefficient. In 3x², 3 is the coefficient, and 2 is the exponent, indicating that x is multiplied by itself twice (x*x).
The expression 3x² represents a term. A term can be a single number, a variable, or a combination of numbers and variables multiplied together. Our expression, 3x² + 3x², consists of two terms, both of which are like terms.
What are Like Terms?
Like terms are terms that have the same variables raised to the same powers. This is crucial for simplification. In our expression, 3x² and 3x² are like terms because they both have the variable x raised to the power of 2. If we had an expression like 3x² + 2x, these would not be like terms because the exponents of x are different (2 vs 1, implicitly). Only like terms can be combined.
Simplifying 3x² + 3x²: A Step-by-Step Approach
Simplifying algebraic expressions involves combining like terms. This is achieved by adding or subtracting the coefficients of the like terms while keeping the variables and their exponents the same. Let's simplify 3x² + 3x² step-by-step:
-
Identify Like Terms: We have two terms, 3x² and 3x². These are like terms because they both contain x²
-
Add the Coefficients: The coefficients of the like terms are 3 and 3. We add these together: 3 + 3 = 6
-
Retain the Variable and Exponent: The variable and its exponent remain unchanged. Therefore, we retain x².
-
Combine: Combining the results from steps 2 and 3, we get 6x².
Therefore, the simplified form of 3x² + 3x² is 6x².
The Distributive Property and its Relevance
While the above method is straightforward, it’s insightful to also understand the problem through the lens of the distributive property. The distributive property states that a(b + c) = ab + ac. Though not immediately apparent, we can apply this to our expression:
We can consider the common factor x² as a "b" in our distributive property example and the coefficients 3 and 3 as our a's and c's. Then, factor out the common term x²:
x²(3 + 3) = x²(6) = 6x²
This method clearly illustrates that we're essentially factoring out the common term and then performing the addition on the coefficients. This understanding deepens your grasp of algebraic manipulation and proves particularly useful when dealing with more complex expressions.
Expanding on the Concept: More Complex Examples
Let's consider slightly more complicated examples to solidify your understanding:
- Example 1: 5x²y + 2x²y - x²y
Here, all three terms are like terms (x²y). We add the coefficients: 5 + 2 - 1 = 6. Therefore, the simplified expression is 6x²y.
- Example 2: 4x³ + 2x² + 3x³ - x²
In this example, we have two sets of like terms: 4x³ and 3x³, and 2x² and -x².
First, we combine the x³ terms: 4x³ + 3x³ = 7x³
Next, we combine the x² terms: 2x² - x² = x² (remember that the coefficient of -x² is -1).
Therefore, the simplified expression is 7x³ + x².
Why is Simplifying Algebraic Expressions Important?
Simplifying algebraic expressions is a fundamental skill in mathematics and is crucial for several reasons:
-
Solving Equations: Simplifying expressions makes solving equations significantly easier. A simplified expression provides a clearer and more manageable form for manipulation.
-
Problem Solving: Many real-world problems, in fields like physics, engineering, and finance, involve solving equations that are initially expressed in complex algebraic forms. Simplifying these expressions helps in developing efficient solutions.
-
Understanding Relationships: Simplified algebraic expressions reveal the relationships between variables more clearly. This facilitates better understanding and interpretation of data or models.
-
Building a Foundation: Mastering simplification builds a robust foundation for more advanced algebraic concepts such as factoring, expanding, solving quadratic equations and beyond.
Frequently Asked Questions (FAQ)
Q1: What if the terms aren't like terms?
A1: If the terms are not like terms (different variables or different exponents), you cannot combine them directly. For example, 3x² + 2x cannot be simplified further. They remain as separate terms.
Q2: Can I simplify 3x² + 3x?
A2: No, you cannot simplify 3x² + 3x because they are unlike terms. They have the same variable (x) but different exponents (2 and 1).
Q3: What happens if the coefficients are negative?
A3: Follow the same rules of addition and subtraction for integers. For example, 5x² - 2x² = 3x², and -4x + 7x = 3x.
Q4: Is there a limit to the number of like terms I can combine?
A4: No, there is no limit. You can combine as many like terms as the expression contains, as long as they share the same variable(s) and exponents.
Q5: What if I have an expression with more than one variable?
A5: The principle remains the same. Combine like terms that have the exact same variables raised to the same powers. For example, in 2xy² + 5xy² – xy², you would combine to get 6xy².
Conclusion
Simplifying algebraic expressions, particularly combining like terms, is a fundamental skill in algebra. The seemingly simple expression 3x² + 3x² provides an excellent introduction to this key concept. By understanding the process of identifying like terms, adding their coefficients, and retaining the variable and its exponent, you develop a foundation for more advanced algebraic manipulation. Remember to practice regularly to solidify your understanding and build confidence in handling more complex expressions. This process forms the bedrock for success in algebra and many other related mathematical disciplines. By mastering this, you open doors to a deeper appreciation and understanding of the power of algebraic manipulation.
Latest Posts
Latest Posts
-
120 Days How Many Months
Sep 15, 2025
-
Busco Una Orquesta Que Salsa
Sep 15, 2025
-
X 2 2x 8 0
Sep 15, 2025
-
How Many Letters In Supercalifragilisticexpialidocious
Sep 15, 2025
-
Is 5 16 Bigger Than 1 2
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Simplify 3x 2 3x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.