What Is 1/4 Of 12
cibeltiagestion
Sep 07, 2025 · 6 min read
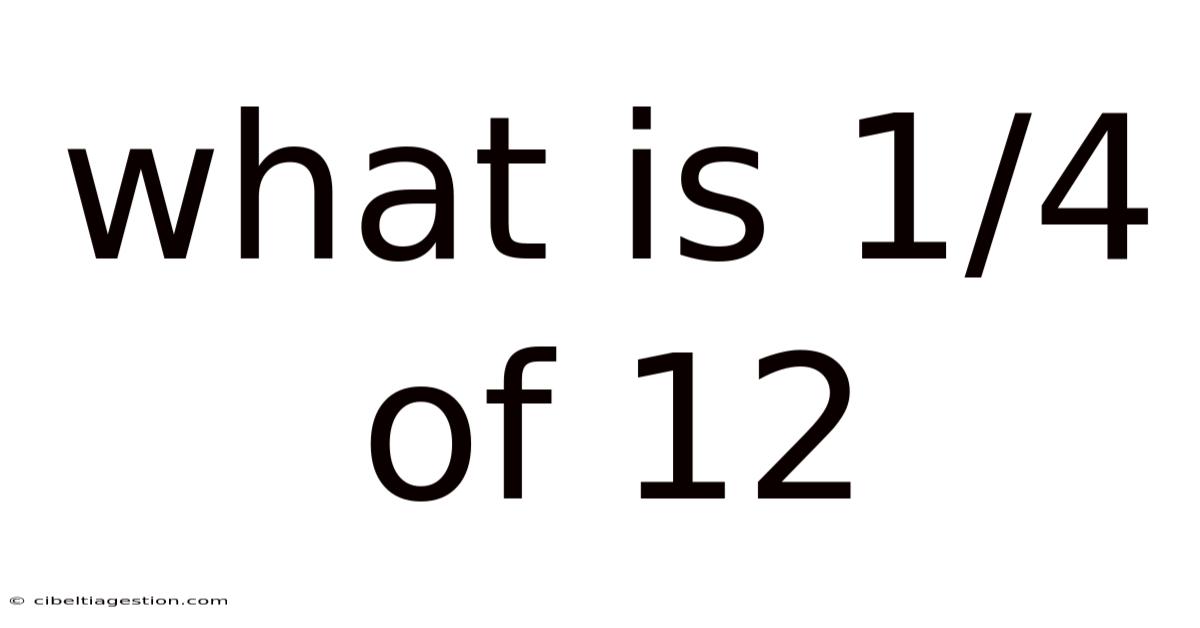
Table of Contents
What is 1/4 of 12? A Deep Dive into Fractions and Multiplication
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will comprehensively explore the question, "What is 1/4 of 12?", delving beyond the simple answer to provide a deeper understanding of fractions, their representation, and the process of multiplication involving fractions. We'll cover various methods for solving this problem, explore its practical applications, and address frequently asked questions. This detailed explanation will equip you with the confidence to tackle similar fraction problems and enhance your overall mathematical understanding.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. For example, in the fraction 1/4, the denominator (4) signifies that the whole is divided into four equal parts, and the numerator (1) indicates that we are considering one of those parts.
Calculating 1/4 of 12: Three Methods
There are several ways to calculate 1/4 of 12. Let's explore three common approaches:
Method 1: Using Multiplication
The most straightforward method is to interpret "of" as multiplication. Therefore, "1/4 of 12" translates to (1/4) x 12. To multiply a fraction by a whole number, we multiply the numerator by the whole number and keep the denominator the same:
(1/4) x 12 = (1 x 12) / 4 = 12/4
Now, we simplify the fraction by dividing the numerator by the denominator:
12/4 = 3
Therefore, 1/4 of 12 is 3.
Method 2: Dividing by the Denominator
Another approach involves understanding that finding a fraction of a number is essentially dividing that number by the denominator and then multiplying by the numerator. In this case:
- Divide by the denominator: 12 ÷ 4 = 3
- Multiply by the numerator: 3 x 1 = 3
This method highlights the inverse relationship between multiplication and division in the context of fractions. It emphasizes that finding 1/4 of something is the same as dividing it into four equal parts.
Method 3: Visual Representation
Visualizing the problem can make it easier to grasp. Imagine a pizza cut into 12 slices. To find 1/4 of the pizza, we divide the 12 slices into four equal groups. Each group will contain:
12 slices ÷ 4 groups = 3 slices per group
Therefore, 1/4 of the pizza (or 1/4 of 12) is 3 slices. This visual method helps solidify the concept of fractions and their practical application.
Beyond the Calculation: Understanding the Concept
While finding the answer (3) is important, understanding why the answer is 3 is even more crucial. This involves a deep understanding of the relationship between fractions, whole numbers, and the concept of parts of a whole.
The fraction 1/4 represents one part out of four equal parts. When we say "1/4 of 12," we're asking for one of the four equal parts of 12. This requires dividing the whole (12) into four equal parts and then taking one of those parts. This division yields the answer 3.
Practical Applications
Understanding fractions and their application is essential in various real-life scenarios:
- Cooking: Recipes often require fractional measurements (e.g., 1/2 cup of flour, 1/4 teaspoon of salt).
- Shopping: Sales often involve discounts expressed as fractions (e.g., 1/3 off).
- Construction: Measurements in building and carpentry frequently use fractions (e.g., 1/4 inch).
- Data Analysis: Fractions are ubiquitous in statistics and data interpretation.
- Finance: Understanding fractions is critical for working with percentages, interest rates, and investments.
Expanding the Concept: Working with Different Fractions
The principles discussed above can be applied to other fraction problems. For instance, let's explore finding 3/4 of 12:
- Divide by the denominator: 12 ÷ 4 = 3
- Multiply by the numerator: 3 x 3 = 9
Therefore, 3/4 of 12 is 9. This demonstrates the adaptability of these methods to different fractional values.
Working with Mixed Numbers
A mixed number combines a whole number and a fraction (e.g., 2 1/2). Let’s explore how to find 1/4 of a mixed number, say 2 1/2:
- Convert the mixed number to an improper fraction: 2 1/2 = (2 x 2 + 1) / 2 = 5/2
- Multiply the fractions: (1/4) x (5/2) = (1 x 5) / (4 x 2) = 5/8
Therefore, 1/4 of 2 1/2 is 5/8. This example showcases the process of handling mixed numbers in fractional calculations.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of a fraction?
A1: The simplest form of a fraction is when the numerator and denominator have no common factors other than 1. For example, 12/4 simplifies to 3/1, or simply 3.
Q2: How do I convert a fraction to a decimal?
A2: To convert a fraction to a decimal, divide the numerator by the denominator. For example, 1/4 = 1 ÷ 4 = 0.25
Q3: How do I convert a decimal to a fraction?
A3: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (e.g., 0.25 = 25/100). Then, simplify the fraction to its lowest terms.
Q4: What are equivalent fractions?
A4: Equivalent fractions represent the same value but have different numerators and denominators. For example, 1/2, 2/4, and 3/6 are all equivalent fractions.
Q5: Can I use a calculator to solve fraction problems?
A5: Yes, most calculators have functions to handle fractions and perform calculations involving fractions. However, understanding the underlying principles is crucial for problem-solving and conceptual understanding.
Conclusion: Mastering Fractions for a Brighter Future
This in-depth exploration of "What is 1/4 of 12?" has moved beyond a simple numerical answer. We’ve delved into the fundamental concepts of fractions, explored multiple solution methods, and highlighted the practical applications of fractional arithmetic. Mastering fractions is not just about memorizing formulas; it's about understanding the underlying principles of parts of a whole, division, and multiplication. By grasping these concepts, you build a strong foundation for more advanced mathematical concepts and equip yourself with a vital skill for navigating various aspects of life. Remember, practice is key! The more you work with fractions, the more comfortable and confident you'll become. So, grab a pencil and paper and start practicing!
Latest Posts
Latest Posts
-
What Is Equivalent To 2 5
Sep 07, 2025
-
How Tall Is 62 Inches
Sep 07, 2025
-
Tango And Cash The Movie
Sep 07, 2025
-
Inputs And Outputs Of Etc
Sep 07, 2025
-
Average Percentage Alcohol In Beer
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.