What Is 15 Of 20
cibeltiagestion
Sep 10, 2025 · 5 min read
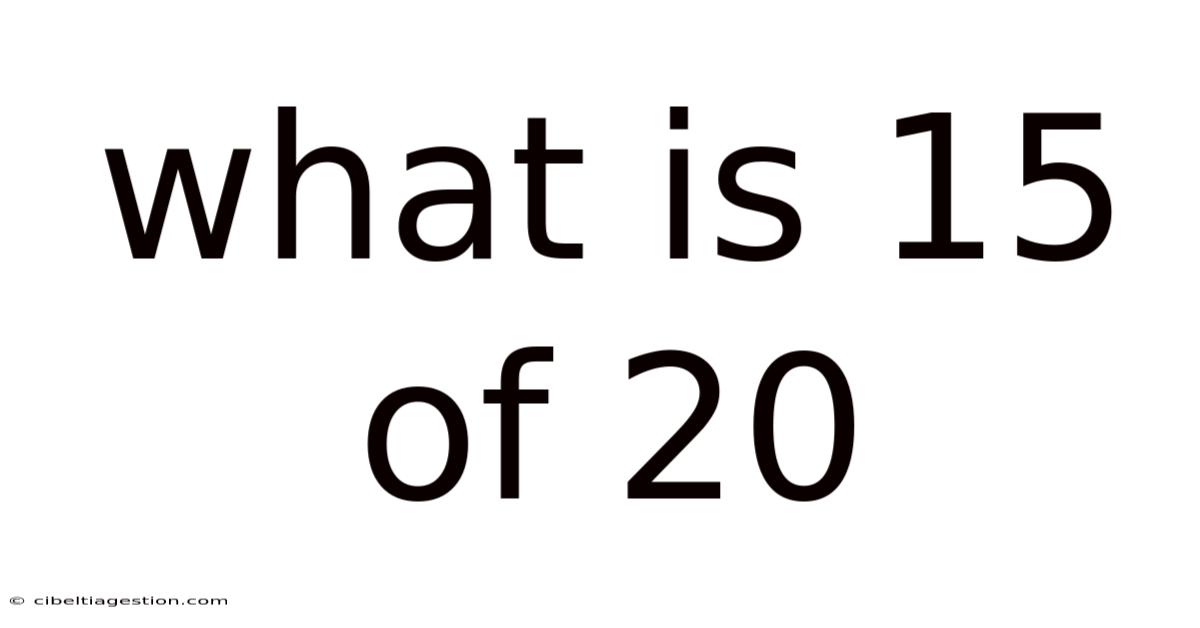
Table of Contents
What is 15 out of 20? Understanding Fractions, Percentages, and Ratios
This article will explore the question "What is 15 out of 20?" in detail, going beyond a simple numerical answer to provide a comprehensive understanding of fractions, percentages, and ratios. We will delve into the practical applications of these mathematical concepts and explore how they are used in everyday life. This understanding is crucial for various aspects of life, from academic pursuits to financial planning and everyday decision-making. Learning to interpret and utilize these concepts empowers you to analyze data, solve problems, and make informed choices.
Understanding Fractions: The Building Blocks
The expression "15 out of 20" is fundamentally a fraction. A fraction represents a part of a whole. In this case, 15 represents the part, and 20 represents the whole. We write this fraction as 15/20.
- Numerator: The top number (15) is called the numerator. It indicates the number of parts we are considering.
- Denominator: The bottom number (20) is called the denominator. It represents the total number of equal parts that make up the whole.
The fraction 15/20 can be simplified by finding the greatest common divisor (GCD) of both the numerator and denominator. The GCD of 15 and 20 is 5. Dividing both the numerator and the denominator by 5, we get:
15 ÷ 5 / 20 ÷ 5 = 3/4
Therefore, 15 out of 20 is equivalent to 3/4. This simplified fraction represents the same proportion but is easier to work with.
Converting Fractions to Percentages: A Common Expression
Percentages are a way of expressing a fraction as a proportion of 100. To convert a fraction to a percentage, we multiply the fraction by 100%. Let's convert 3/4 (or 15/20) to a percentage:
(3/4) * 100% = 75%
Therefore, 15 out of 20 is equal to 75%. This is a more readily understandable representation for many people, allowing for quick comparisons and estimations. A score of 75% on a test, for instance, is easily understood as a good performance, even without knowing the total number of questions.
Understanding Ratios: Comparing Quantities
A ratio is a comparison of two or more quantities. The ratio of 15 to 20 can be written in several ways:
- 15:20
- 15/20
- 15 to 20
Similar to fractions, ratios can be simplified by finding the GCD. Simplifying the ratio 15:20 gives us the ratio 3:4. This means that for every 3 parts of one quantity, there are 4 parts of another. Ratios are used extensively in various fields, including cooking (e.g., a recipe might call for a 2:1 ratio of flour to sugar), map-making (scale ratios), and many scientific and engineering applications.
Practical Applications: Real-World Examples
Understanding fractions, percentages, and ratios is essential in various real-world scenarios:
- Academic Performance: A student scoring 15 out of 20 on a test achieved 75%, indicating a good understanding of the subject matter.
- Financial Matters: Calculating interest rates, discounts, and tax percentages all rely on fractional and percentage calculations. Understanding proportions helps in budget management and investment decisions.
- Cooking and Baking: Recipes frequently utilize ratios for ingredient proportions. Understanding ratios ensures consistent and successful outcomes.
- Sports Statistics: Batting averages, win-loss ratios, and other sports statistics heavily utilize fractions and percentages to represent a player's or team's performance.
- Scientific Research: Many scientific concepts and data analysis rely on ratios and proportions to understand relationships between different variables.
Further Exploration: Working with Fractions
While we've simplified 15/20 to 3/4, let's look at other ways to approach fractions:
Adding and Subtracting Fractions: To add or subtract fractions, they must have a common denominator. If we needed to add 15/20 to another fraction, we might first simplify 15/20 to 3/4 and then find a common denominator with the other fraction.
Multiplying and Dividing Fractions: Multiplying fractions involves multiplying the numerators and multiplying the denominators. Dividing fractions involves inverting the second fraction and then multiplying. These operations are crucial for many calculations in various fields.
Frequently Asked Questions (FAQ)
Q: Can I express 15 out of 20 as a decimal?
A: Yes, you can convert the fraction 3/4 (or 15/20) to a decimal by dividing the numerator by the denominator: 3 ÷ 4 = 0.75
Q: What if the numbers weren't so easily divisible?
A: If the numbers were more complex, you would still follow the same principles. Find the GCD to simplify the fraction, convert to a percentage by multiplying by 100%, and express it as a decimal by performing the division. Using a calculator can simplify the process for larger numbers.
Q: Are percentages always more helpful than fractions?
A: Not necessarily. Percentages are great for quick comparisons and general understanding, but fractions offer a more precise representation in many contexts, especially when dealing with detailed calculations or specialized fields. Both have their uses, and the best representation depends on the context.
Q: How do I know which method (fraction, percentage, ratio, or decimal) to use?
A: The best method depends on the specific situation and what you want to communicate. Consider the context, the audience, and the type of information you want to convey. Sometimes a combination of methods can provide the clearest picture.
Conclusion: Mastering the Fundamentals
Understanding "what is 15 out of 20?" extends far beyond a simple numerical answer. It involves grasping the core concepts of fractions, percentages, and ratios, and their interrelationships. These fundamental mathematical concepts are not just academic exercises; they are essential tools for navigating various aspects of everyday life, from managing finances to interpreting data and making informed decisions. By mastering these concepts, you equip yourself with the skills necessary for success in numerous fields and empower yourself to confidently tackle numerical challenges. The ability to convert between fractions, percentages, decimals, and ratios enhances analytical skills and opens doors to a deeper understanding of the quantitative world around us.
Latest Posts
Latest Posts
-
What Do Blood Taste Like
Sep 10, 2025
-
Wingdings Font Character Code 110
Sep 10, 2025
-
1 8 Divided 3 4
Sep 10, 2025
-
4 5 Million Yen To Usd
Sep 10, 2025
-
5 2 Independent Practice Answer Key
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.