What Is -20/3 Whole Number
cibeltiagestion
Sep 11, 2025 · 5 min read
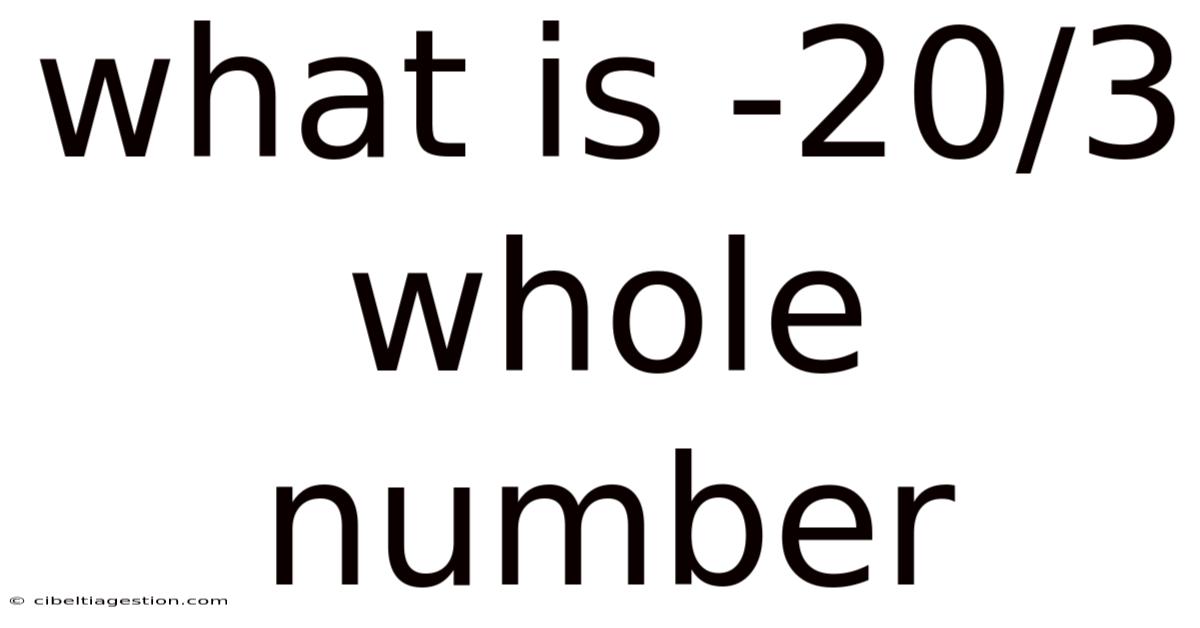
Table of Contents
What is -20/3 as a Whole Number? Understanding Fractions and Integers
Many mathematical problems involve converting fractions into whole numbers or integers. This seemingly simple task can be confusing, especially when dealing with negative fractions like -20/3. This article will comprehensively explain how to approach this problem, explore the concept of whole numbers and integers, and clarify why -20/3 cannot be directly expressed as a whole number. We will delve into the process of converting fractions to decimals and then consider the implications for rounding and approximation. By the end, you'll have a solid understanding of fractions, integers, and how to handle situations like this confidently.
Introduction to Whole Numbers and Integers
Before tackling -20/3, let's establish a firm understanding of the key terms involved: whole numbers and integers.
-
Whole Numbers: These are the numbers 0, 1, 2, 3, and so on. They are non-negative and don't include fractions or decimals. Think of them as counting numbers, starting from zero.
-
Integers: This set includes all whole numbers, plus their negative counterparts. So, integers are ..., -3, -2, -1, 0, 1, 2, 3, ... They extend infinitely in both positive and negative directions.
The crucial difference lies in the inclusion of negative numbers. Whole numbers are a subset of integers. Understanding this distinction is vital for grasping the limitations of expressing -20/3 as a whole number.
Understanding Fractions: Numerator, Denominator, and Division
A fraction represents a part of a whole. It's composed of two parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
The fraction -20/3 means we have -20 parts of a whole that's been divided into 3 equal parts. The negative sign signifies a negative quantity. Fractions inherently represent portions, not necessarily whole units.
Converting -20/3 to a Decimal
To better understand the value of -20/3, we can convert it to a decimal. This involves performing the division:
-20 ÷ 3 = -6.666...
The result is a repeating decimal, specifically -6.666..., where the '6' repeats infinitely. This decimal representation highlights why -20/3 cannot be expressed as a whole number. Whole numbers, by definition, do not have fractional or decimal parts.
Why -20/3 Cannot Be a Whole Number
The fundamental reason -20/3 can't be a whole number is the remainder after the division. When we divide -20 by 3, we get -6 with a remainder of -2. Whole numbers don't have remainders; they represent complete units. The remainder of -2 indicates that we're missing two-thirds of a unit to reach the next whole number. This fractional part prevents -20/3 from being classified as a whole number.
Approximations and Rounding
While -20/3 is not a whole number, we can approximate it. This involves rounding the decimal representation (-6.666...) to the nearest whole number.
- Rounding down: This gives us -7.
- Rounding up: This gives us -6.
The choice between rounding up or down depends on the context of the problem. In some cases, rounding down might be more appropriate to represent a conservative estimate, while rounding up might be suitable in other situations. However, it's essential to remember that these are approximations, and the result is not exactly equal to -20/3.
Illustrative Examples
Let's consider a few examples to solidify our understanding:
Example 1: Imagine you owe someone 20 dollars, and you decide to pay them back in three equal installments. Each installment would be -20/3 dollars, which is approximately -6.67 dollars (rounded to two decimal places). You can't pay in whole dollar amounts and exactly settle the debt; you will always have a remainder.
Example 2: You're measuring the length of a piece of wood. The wood measures -20/3 centimeters. This is a negative length (possibly representing a measurement relative to a reference point), and its precise value is -6.666... centimeters. You can approximate this length as -7 cm or -6 cm, depending on the level of precision required.
Frequently Asked Questions (FAQ)
Q1: Can any fraction be expressed as a whole number?
A1: No. Only fractions where the numerator is a multiple of the denominator can be expressed as a whole number (or integer if the fraction is negative). For example, -12/3 = -4 (a whole number).
Q2: What's the difference between rounding and truncation?
A2: Rounding considers the value of the digit after the decimal point to determine whether to round up or down. Truncation simply removes the digits after the decimal point, regardless of their value. For -20/3, truncation would yield -6.
Q3: How do I represent -20/3 on a number line?
A3: You would place it between -7 and -6, slightly closer to -7, reflecting its decimal value of -6.666...
Q4: Is there a way to express -20/3 without decimals or approximations?
A4: Yes, you can express it as the mixed number -6 ⅔. This form precisely represents the value without resorting to decimals or rounding. It shows the whole number part (-6) and the fractional part (⅔).
Conclusion: Precision vs. Approximation
In conclusion, -20/3 cannot be expressed as a whole number because the division results in a repeating decimal with a remainder. While we can approximate its value by rounding to the nearest whole number (-7 or -6), it's crucial to remember that this is an approximation, not an exact representation. The precise value remains -20/3, or its equivalent mixed number form, -6 ⅔. Understanding this distinction is vital for accurate mathematical calculations and interpreting results in real-world applications. The key takeaway is to embrace the fractional representation when precision is necessary, and utilize approximation techniques only when the context allows for a degree of uncertainty.
Latest Posts
Latest Posts
-
Computer Parts You Can Touch
Sep 12, 2025
-
4 Ft 3 In Inches
Sep 12, 2025
-
What Is 75 Of 27
Sep 12, 2025
-
How Many Ml Is 16oz
Sep 12, 2025
-
Ms Florina Buys A Bag
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is -20/3 Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.