What Is 75 Of 27
cibeltiagestion
Sep 12, 2025 · 5 min read
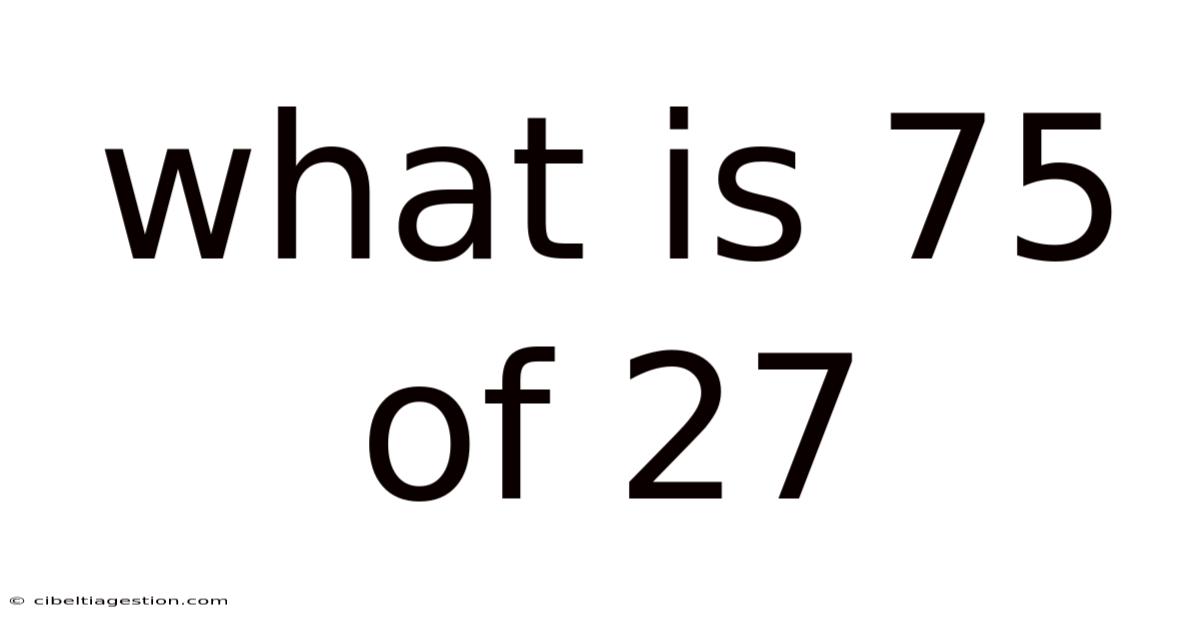
Table of Contents
What is 75% of 27? A Comprehensive Guide to Percentages and Their Applications
Finding 75% of 27 might seem like a simple calculation, but it opens the door to understanding a fundamental mathematical concept with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This article will not only show you how to calculate 75% of 27 but also delve into the underlying principles of percentages, providing you with the tools to tackle similar problems with confidence. We'll explore various methods, explain the underlying math, and even touch upon real-world examples.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 75% means 75 out of 100, or 75/100. This fraction can be simplified to 3/4. Understanding this basic concept is crucial for tackling percentage calculations.
Method 1: Converting the Percentage to a Decimal
This is perhaps the most straightforward method. To find 75% of 27, we first convert the percentage to its decimal equivalent. We do this by dividing the percentage by 100:
75% ÷ 100 = 0.75
Now, we multiply this decimal by the number we're finding the percentage of (27):
0.75 * 27 = 20.25
Therefore, 75% of 27 is 20.25.
Method 2: Using Fractions
As mentioned earlier, 75% can be expressed as the fraction 3/4. This method involves multiplying the fraction by the number:
(3/4) * 27 = 81/4
To convert this improper fraction to a decimal, we divide the numerator (81) by the denominator (4):
81 ÷ 4 = 20.25
Again, we arrive at the answer: 75% of 27 is 20.25.
Method 3: Breaking Down the Percentage
This method is helpful for mental calculations or when dealing with less straightforward percentages. We can break down 75% into smaller, easier-to-manage percentages. For instance:
- 50% of 27: Half of 27 is 13.5
- 25% of 27: A quarter of 27 is 6.75 (this is half of 50% of 27)
Adding these together: 13.5 + 6.75 = 20.25
This illustrates that 75% (50% + 25%) of 27 is 20.25.
The Math Behind Percentages: A Deeper Dive
The core mathematical operation behind percentage calculations is multiplication. When we find a percentage of a number, we're essentially finding a fraction of that number. The formula is:
Percentage * Number = Result
Where:
- Percentage is the percentage expressed as a decimal (e.g., 75% = 0.75)
- Number is the value you're finding the percentage of (e.g., 27)
- Result is the answer you're looking for
This formula is applicable to all percentage calculations, regardless of the complexity.
Real-World Applications of Percentage Calculations
Understanding percentages is vital in numerous real-world situations:
- Discounts: Retailers often advertise discounts as percentages. If a store offers a 25% discount on an item priced at $50, you would calculate 25% of $50 to determine the discount amount and then subtract it from the original price.
- Taxes: Sales tax is usually expressed as a percentage of the purchase price. Calculating the tax amount requires finding the percentage of the total cost.
- Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding how to calculate interest is fundamental to financial planning.
- Tips and Gratuities: Restaurants often suggest a percentage tip (e.g., 15%, 20%) for good service.
- Grade Calculations: Your final grade in a course often involves calculating your weighted average, where individual assignments are weighted by percentages.
- Data Analysis: In statistics and data analysis, percentages are used extensively to represent proportions and changes in data.
- Finance: Financial statements frequently use percentages to express ratios and trends in a company's performance (e.g., profit margins, debt-to-equity ratio).
- Science and Engineering: Percentages are used in many scientific and engineering calculations, often to express error margins, efficiency levels, or concentration levels.
Beyond the Basics: More Complex Percentage Problems
While finding 75% of 27 is a relatively simple calculation, the principles extend to more complex scenarios. For example:
- Finding the original amount: If you know the percentage and the resulting value, you can work backward to find the original amount.
- Finding the percentage increase or decrease: This involves comparing two values and calculating the percentage change between them.
- Compound interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding compound interest is crucial for long-term financial planning.
- Percentage points: A percentage point refers to an absolute change in percentage values, not a relative change. For instance, a change from 10% to 15% is a five percentage point increase, not a 50% increase.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase?
- A: Subtract the original value from the new value. Then, divide the result by the original value and multiply by 100 to express the change as a percentage.
-
Q: How do I calculate a percentage decrease?
- A: Subtract the new value from the original value. Then, divide the result by the original value and multiply by 100.
-
Q: What if the percentage is greater than 100%?
- A: This simply means the resulting value is greater than the original value. For instance, 150% of 27 is (1.5 * 27) = 40.5.
-
Q: Can I use a calculator for percentage calculations?
- A: Yes, most calculators have a percentage function (%) that simplifies these calculations. However, understanding the underlying principles remains crucial.
-
Q: Are there any online resources or tools to help with percentage calculations?
- A: Numerous online calculators and resources are available to assist with percentage calculations of varying complexity.
Conclusion: Mastering Percentages for Life
Finding 75% of 27, while seemingly a simple task, provides a strong foundation for understanding the broader world of percentage calculations. By grasping the fundamental principles outlined in this article—converting percentages to decimals or fractions, applying the core multiplication formula, and breaking down complex problems into smaller, manageable steps—you'll be well-equipped to handle various percentage-related challenges in your personal and professional life. Remember, the key is not just to find the answer but to understand the why behind the calculation, allowing you to apply these skills confidently and effectively in any situation. The ability to confidently work with percentages is an invaluable skill that will serve you well in many aspects of life.
Latest Posts
Latest Posts
-
Find The Sum 6 X 4 5 X
Sep 12, 2025
-
Is Bes Ges If So
Sep 12, 2025
-
How Long Is 10 Millimeters
Sep 12, 2025
-
1 2x 5 4x 3
Sep 12, 2025
-
21st Letter Of The Alphabet
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.