What Is 30 Of 120
cibeltiagestion
Sep 07, 2025 · 6 min read
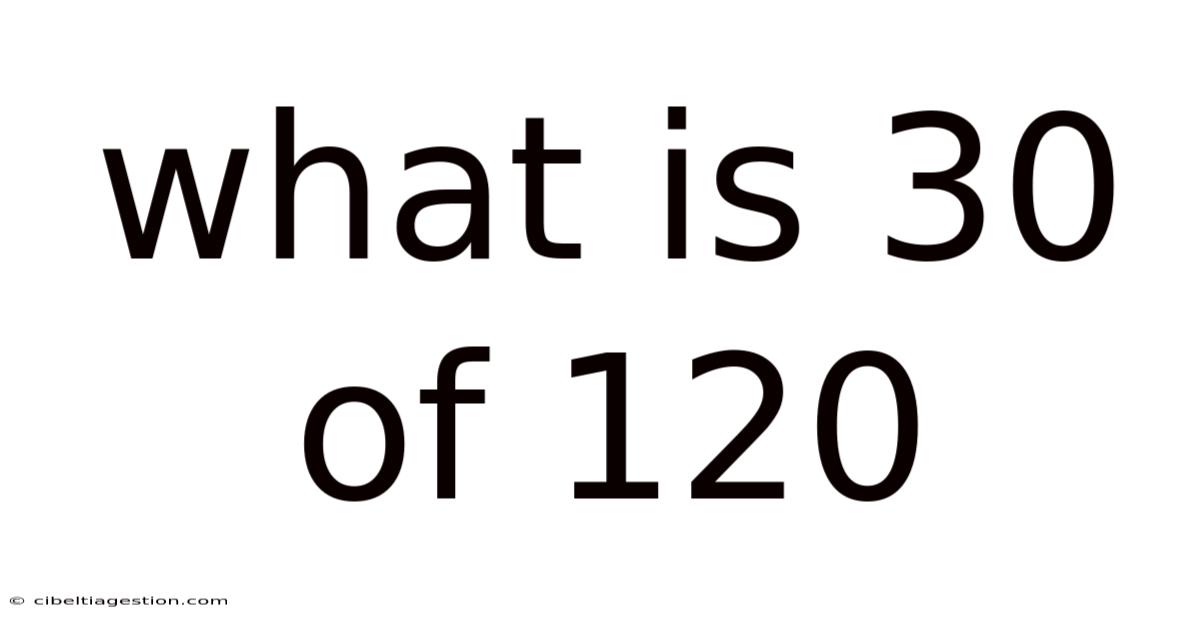
Table of Contents
What is 30 of 120? Understanding Fractions, Percentages, and Ratios
This article explores the question, "What is 30 of 120?", delving far beyond a simple numerical answer. We'll dissect this problem using different mathematical approaches, highlighting the concepts of fractions, percentages, and ratios, and demonstrating their practical applications. Understanding these core mathematical concepts is crucial for navigating everyday life, from calculating discounts to understanding financial reports. This comprehensive guide provides a clear and intuitive understanding for learners of all levels.
Introduction: More Than Just a Calculation
At first glance, "What is 30 of 120?" seems like a straightforward question. A simple calculator will tell you that 30 is a part of 120. However, understanding how 30 relates to 120 unlocks a deeper understanding of fundamental mathematical principles. We'll explore this relationship through the lenses of fractions, percentages, and ratios, showing how these interconnected concepts provide different perspectives on the same problem.
Understanding Fractions: Parts of a Whole
The most direct way to represent 30 out of 120 is as a fraction: 30/120. A fraction represents a part of a whole. In this case, 30 represents the part, and 120 represents the whole.
-
Simplifying Fractions: This fraction can be simplified by finding the greatest common divisor (GCD) of 30 and 120. The GCD is 30. Dividing both the numerator (30) and the denominator (120) by 30 gives us the simplified fraction 1/4. This means 30 is one-quarter (1/4) of 120.
-
Visualizing Fractions: Imagine a pizza cut into 120 slices. If you take 30 slices, you've taken 1/4 of the pizza. This visual representation helps solidify the understanding of what the fraction represents.
-
Practical Applications of Fractions: Fractions are used extensively in various fields. From measuring ingredients in cooking (1/2 cup of flour) to understanding probabilities (1/6 chance of rolling a specific number on a die), fractions are fundamental to expressing parts of a whole.
Calculating Percentages: Expressing Parts per Hundred
Percentages provide another way to express the relationship between 30 and 120. A percentage represents a fraction where the denominator is 100. To convert the fraction 30/120 to a percentage, we perform the following calculation:
(30/120) * 100% = 25%
This means 30 is 25% of 120.
-
Understanding Percentage Calculations: The formula for calculating percentages is: (Part/Whole) * 100%. This formula is widely used in various applications, including calculating discounts, interest rates, and tax percentages.
-
Practical Applications of Percentages: Percentages are ubiquitous in everyday life. We encounter them when calculating sales tax, understanding interest rates on loans, analyzing statistical data, and assessing performance metrics.
Exploring Ratios: Comparing Quantities
A ratio expresses the quantitative relationship between two or more amounts. The ratio of 30 to 120 can be written as 30:120 or 30/120. Similar to fractions, ratios can be simplified. Simplifying the ratio 30:120 by dividing both terms by 30 gives us the simplified ratio 1:4.
-
Interpreting Ratios: This simplified ratio, 1:4, means that for every one unit of the first quantity (30), there are four units of the second quantity (120).
-
Practical Applications of Ratios: Ratios are essential in various fields, such as scaling recipes in cooking (a 1:2 ratio of sugar to flour), mixing ingredients in chemistry (a specific ratio of reactants), and comparing financial data.
The Interconnectedness of Fractions, Percentages, and Ratios
It's important to note that fractions, percentages, and ratios are closely related. They all represent ways of expressing the relationship between parts and wholes or different quantities. They can be converted from one form to another, allowing for flexibility in expressing and understanding quantitative relationships. For instance:
- A fraction can be converted to a percentage by multiplying by 100%.
- A percentage can be converted to a fraction by dividing by 100% and simplifying.
- A ratio can be expressed as a fraction by placing one quantity over the other.
The ability to move fluidly between these representations enhances mathematical problem-solving skills.
Solving Similar Problems: Applying the Concepts
Let's apply the principles we've learned to solve similar problems. Suppose we want to find:
-
What is 15 of 60? This is equivalent to the fraction 15/60, which simplifies to 1/4 or 25%. The ratio is 1:4.
-
What is 40 of 200? This is represented by the fraction 40/200, simplifying to 1/5 or 20%. The ratio is 1:5.
-
What is 75 of 300? This translates to 75/300, which simplifies to 1/4 or 25%. The ratio is 1:4.
By consistently applying the concepts of fractions, percentages, and ratios, we can efficiently solve a wide range of problems involving parts and wholes, comparisons, and proportions.
Real-World Applications: Beyond the Classroom
The practical applications of understanding fractions, percentages, and ratios extend far beyond academic settings. Here are a few examples:
- Finance: Calculating interest rates, discounts, taxes, and analyzing financial statements.
- Cooking: Scaling recipes, adjusting ingredient quantities.
- Construction: Measuring materials, scaling blueprints.
- Data Analysis: Understanding proportions and distributions in statistical data.
- Retail: Calculating sales, discounts, and profits.
- Science: Expressing concentrations, ratios of substances in chemical reactions.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to find a percentage of a number?
A1: The easiest way is to use the formula: (Part/Whole) * 100%. For example, to find 20% of 80: (20/100) * 80 = 16.
Q2: How do I simplify a fraction?
A2: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator. Divide both the numerator and the denominator by the GCD. For example, to simplify 12/18, the GCD is 6. Dividing both by 6 gives 2/3.
Q3: What is the difference between a ratio and a fraction?
A3: While both express relationships between quantities, a fraction always represents a part of a whole, while a ratio compares two or more quantities. However, a ratio can be expressed as a fraction.
Q4: How can I improve my understanding of these concepts?
A4: Practice is key! Solve various problems involving fractions, percentages, and ratios. Use visual aids like diagrams and charts to solidify your understanding. Seek help from teachers, tutors, or online resources when needed.
Conclusion: Mastering Fundamental Mathematical Concepts
Understanding "what is 30 of 120" is not merely about arriving at the answer 25%. It's about grasping the underlying mathematical concepts – fractions, percentages, and ratios – and their interconnectedness. Mastering these concepts equips you with valuable tools for tackling a wide range of problems in everyday life, from personal finance to professional endeavors. By consistently practicing and applying these principles, you can confidently navigate the world of numbers and confidently solve problems that involve parts and wholes, proportions, and comparisons. The journey to mastering these concepts is not just about memorizing formulas; it's about developing a deeper understanding of how numbers relate to each other, and how these relationships can be used to solve real-world problems.
Latest Posts
Latest Posts
-
101 Degrees Fahrenheit In Celsius
Sep 08, 2025
-
Percent Of 4 Is 7
Sep 08, 2025
-
Ttp Medical Abbreviation Physical Exam
Sep 08, 2025
-
States That Start With C
Sep 08, 2025
-
212 Degrees Farenheit To Celcius
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.