What Is 35 Of 80
cibeltiagestion
Sep 07, 2025 · 5 min read
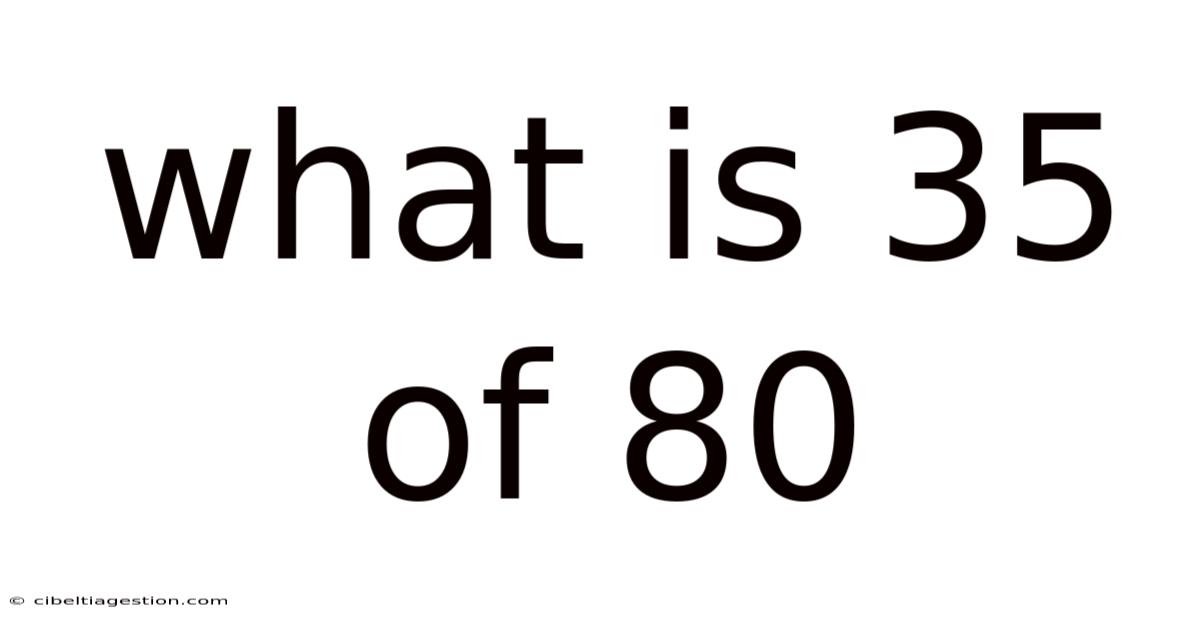
Table of Contents
What is 35/80? Understanding Fractions, Percentages, and Decimals
Finding out "what is 35/80?" might seem like a simple arithmetic problem, but it opens a door to a wider understanding of fractions, percentages, and decimals – essential concepts in mathematics and everyday life. This article will guide you through the process of solving this problem and explore the interconnectedness of these numerical representations. We'll delve into the methods of simplification, conversion, and practical applications, ensuring a comprehensive understanding for learners of all levels.
Introduction: Deconstructing the Fraction 35/80
The expression "35/80" represents a fraction. A fraction shows a part of a whole. In this case, 35 represents the part, and 80 represents the whole. Understanding this basic structure is crucial before proceeding to calculations. This article will not only calculate the value of 35/80 but also explore various methods to represent this fraction, showcasing the versatility of mathematical representation. We'll cover simplification, conversion to decimals and percentages, and finally discuss some real-world applications of this type of calculation.
Step-by-Step Calculation: Simplifying 35/80
The first step in understanding 35/80 is to simplify the fraction. Simplifying a fraction means reducing it to its lowest terms, making it easier to work with and understand. We do this by finding the greatest common divisor (GCD) of both the numerator (35) and the denominator (80).
The GCD is the largest number that divides both 35 and 80 without leaving a remainder. Let's find it using prime factorization:
- 35: The prime factors of 35 are 5 and 7 (5 x 7 = 35).
- 80: The prime factors of 80 are 2 x 2 x 2 x 2 x 5 (2<sup>4</sup> x 5 = 80).
The only common prime factor between 35 and 80 is 5. Therefore, the GCD is 5.
Now, we divide both the numerator and the denominator by the GCD:
35 ÷ 5 = 7 80 ÷ 5 = 16
So, the simplified fraction is 7/16. This is the most concise and efficient way to represent the same portion.
Converting the Fraction to a Decimal
Converting a fraction to a decimal is straightforward. We simply divide the numerator by the denominator:
7 ÷ 16 = 0.4375
Therefore, 35/80, simplified to 7/16, is equal to 0.4375 as a decimal.
Converting the Fraction to a Percentage
To convert a fraction or decimal to a percentage, we multiply by 100%:
0.4375 x 100% = 43.75%
Therefore, 35/80 represents 43.75%. This means that 35 is 43.75% of 80.
Understanding the Interplay: Fractions, Decimals, and Percentages
These three representations – fractions, decimals, and percentages – are interconnected. Each offers a different way of expressing the same proportion. Understanding their relationship is key to mastering basic mathematics. Fractions are fundamental, offering a clear visual representation of parts of a whole. Decimals are useful for calculations and comparisons, while percentages are widely used to express proportions in everyday life, often in contexts like discounts, interest rates, or statistics.
Real-World Applications of Fraction Calculations
The ability to work with fractions, decimals, and percentages isn't confined to the classroom; it's a valuable skill in numerous everyday situations. Here are some examples:
- Cooking and Baking: Recipes often involve fractions (e.g., 1/2 cup of sugar, 3/4 cup of flour). Understanding fractions is vital for accurate measurements and successful cooking.
- Shopping and Budgeting: Calculating discounts, sales tax, and comparing prices often requires working with percentages. For instance, determining the final cost of an item after a 20% discount involves percentage calculations.
- Measurement and Construction: In construction and engineering, precise measurements are paramount. Working with fractions and decimals ensures accuracy in projects.
- Data Analysis and Statistics: Many fields rely on data analysis and statistical interpretation, which heavily uses percentages and proportions to represent information efficiently.
- Finance and Investments: Understanding interest rates, returns on investment, and loan calculations relies heavily on the understanding of percentages and decimals.
Frequently Asked Questions (FAQ)
-
Q: What if I don't know how to find the GCD?
- A: If you're unsure about finding the greatest common divisor, you can use a method called repeated division. Continuously divide both the numerator and denominator by common factors until no further common factors exist. While less efficient for larger numbers, it’s a reliable method for beginners.
-
Q: Are there other ways to convert a fraction to a decimal?
- A: Yes, you could use a calculator, which directly computes the decimal equivalent of a fraction. Alternatively, you can express the fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000). This simplifies the conversion to a decimal. However, this is not always possible.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand and work with. It reduces the size of the numbers, minimizing the complexity of calculations and improving accuracy. A simplified fraction provides a clearer representation of the proportion.
-
Q: Can I use a calculator to find 35/80?
- A: Absolutely! Calculators are helpful tools for performing these types of calculations quickly and accurately. However, understanding the underlying principles remains crucial.
Further Exploration: Expanding Your Mathematical Knowledge
Understanding 35/80 is only the starting point. This problem opens the door to broader mathematical concepts. You can expand your knowledge by exploring:
- More complex fractions: Practice simplifying and converting fractions with larger numerators and denominators.
- Working with mixed numbers: Learn to convert between improper fractions (like 35/80) and mixed numbers (a whole number and a proper fraction).
- Solving equations involving fractions: Progress to solving algebraic equations where fractions are involved.
- Exploring different number systems: Understand the relationships between fractions, decimals, percentages, and other number systems.
Conclusion: Mastering the Fundamentals
The seemingly simple question "What is 35/80?" has led us through a journey of understanding fractions, decimals, and percentages. We discovered that 35/80 simplifies to 7/16, equals 0.4375 as a decimal, and represents 43.75% as a percentage. This exploration highlighted the interconnectedness of these representations and demonstrated their practical applications in various aspects of life. By mastering these fundamental concepts, you equip yourself with essential skills applicable across numerous fields. Remember, the key to success is consistent practice and a willingness to explore further mathematical concepts. So keep practicing and expanding your knowledge—the world of mathematics awaits!
Latest Posts
Latest Posts
-
Cr2 So4 3 Nh4 2co3
Sep 07, 2025
-
Express 0 0939 As A Fraction
Sep 07, 2025
-
Your Brakes Need Checking If
Sep 07, 2025
-
536 Cm To 53 6 Dm
Sep 07, 2025
-
Fecl3 Cocl2 Ionic Equation
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 35 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.