What Is 76 Of 250
cibeltiagestion
Sep 10, 2025 · 5 min read
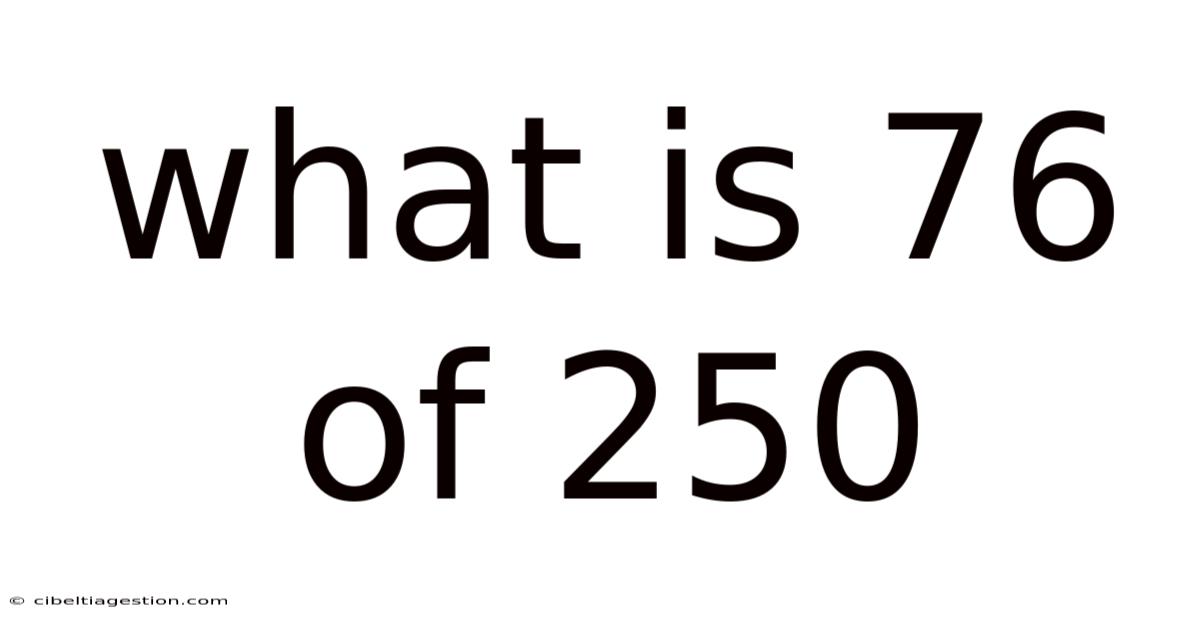
Table of Contents
What is 76% of 250? A Deep Dive into Percentages and Their Applications
Finding a percentage of a number is a fundamental mathematical skill with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article will explore how to calculate 76% of 250, providing a step-by-step guide, explanations of the underlying principles, and demonstrating the versatility of percentage calculations across various fields. We'll also delve into common mistakes and frequently asked questions to ensure a comprehensive understanding of this crucial concept.
Understanding Percentages
Before we tackle the specific calculation of 76% of 250, let's establish a solid foundation in understanding percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 76% can be written as 76/100 or 0.76 in decimal form.
Calculating 76% of 250: The Step-by-Step Approach
There are several ways to calculate 76% of 250. Here are two common methods:
Method 1: Using Decimal Conversion
-
Convert the percentage to a decimal: Divide the percentage by 100. In this case, 76% / 100 = 0.76.
-
Multiply the decimal by the number: Multiply the decimal (0.76) by the number you want to find the percentage of (250). 0.76 * 250 = 190.
Therefore, 76% of 250 is $\boxed{190}$.
Method 2: Using Fractions
-
Convert the percentage to a fraction: Express the percentage as a fraction with a denominator of 100. 76% = 76/100.
-
Simplify the fraction (if possible): Both 76 and 100 are divisible by 4, simplifying the fraction to 19/25.
-
Multiply the fraction by the number: Multiply the simplified fraction (19/25) by the number (250). (19/25) * 250 = 19 * (250/25) = 19 * 10 = 190.
Again, we find that 76% of 250 is $\boxed{190}$.
The Significance of Percentage Calculations
The ability to calculate percentages is crucial in numerous real-world scenarios. Here are a few examples:
-
Finance: Calculating interest on loans, savings accounts, and investments. Determining the discount on sale items, understanding tax rates, and analyzing financial statements all involve percentage calculations.
-
Retail: Calculating discounts, markups, and profit margins. Retailers use percentages to determine selling prices, assess profitability, and offer promotions effectively.
-
Statistics: Representing data as percentages allows for easier comparison and interpretation. Percentages are fundamental in analyzing surveys, polls, and other statistical data. For example, understanding market share often involves working with percentages.
-
Science: In scientific research, percentages are used extensively to express ratios, concentrations, and error margins.
-
Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels, and evaluating the success rate of various endeavors all rely on percentage calculations.
Beyond the Basics: Advanced Percentage Applications
While calculating a simple percentage like 76% of 250 is straightforward, the application of percentages can become more complex. Consider these scenarios:
-
Finding the Percentage One Number Represents of Another: If you sold 190 items out of a total of 250, what percentage did you sell? This involves dividing the part (190) by the whole (250) and multiplying by 100: (190/250) * 100 = 76%.
-
Calculating Percentage Increase or Decrease: If a price increased from 200 to 250, what is the percentage increase? First, find the difference (250 - 200 = 50). Then, divide the difference by the original value (50/200 = 0.25) and multiply by 100 (0.25 * 100 = 25%). The price increased by 25%.
-
Working with Compound Percentages: Compound percentages involve applying a percentage multiple times, such as calculating compound interest over several years. This often requires more advanced mathematical formulas.
-
Solving for Unknown Values: You might encounter problems where you know the percentage and the result, but need to find the original value. For instance, if 76% of a number is 190, what is the number? This requires working backward using algebraic techniques.
Common Mistakes to Avoid
-
Misplacing the decimal point: When converting percentages to decimals, ensure the decimal point is placed correctly. A misplaced decimal can lead to significant errors.
-
Incorrect order of operations: Remember the order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
-
Confusing percentage increase and decrease: Be mindful of whether you are calculating a percentage increase or decrease. The calculation differs slightly depending on whether the value is increasing or decreasing.
-
Using the wrong base value: When calculating percentage increase or decrease, it's crucial to use the original value as the base for the calculation.
Frequently Asked Questions (FAQ)
Q: What are some real-world examples of percentage calculations?
A: Real-world examples are abundant and include calculating sales tax, discounts on purchases, interest on loans and investments, tip amounts at restaurants, and understanding statistics presented in percentages in news reports or scientific studies.
Q: How can I improve my percentage calculation skills?
A: Practice is key! Work through various problems, starting with simple calculations and gradually increasing the complexity. Utilize online resources, calculators, and textbooks to further enhance your understanding.
Q: What if I need to calculate a percentage of a number that is not a whole number?
A: The process remains the same. Convert the percentage to a decimal and multiply it by the given number, regardless of whether the number is a whole number or a decimal.
Q: Are there any online tools or calculators available to help with percentage calculations?
A: Yes, numerous online percentage calculators are readily available that can assist with various percentage calculations.
Q: What is the difference between a percentage and a ratio?
A: A percentage is a specific type of ratio that expresses a proportion out of 100. A ratio, on the other hand, expresses a relationship between two or more quantities. A percentage can be expressed as a ratio, but not all ratios are percentages.
Conclusion
Calculating 76% of 250, which equals 190, is a fundamental application of percentage calculations. Understanding this seemingly simple calculation unlocks a world of possibilities in various fields, from finance and retail to statistics and science. By mastering the techniques and avoiding common pitfalls, you can confidently apply percentage calculations in diverse real-world situations, enhancing your problem-solving skills and numerical literacy. The ability to work with percentages is an invaluable asset in navigating the complexities of modern life. Remember to practice consistently to solidify your understanding and build confidence in tackling more complex percentage-based problems.
Latest Posts
Latest Posts
-
Is Hexane Polar Or Nonpolar
Sep 10, 2025
-
Un Automovilista Debe Saber Que
Sep 10, 2025
-
Square Root Of 20 Simplified
Sep 10, 2025
-
Honest Is To Genuine As
Sep 10, 2025
-
Slider Owns A Hamburger Restaurant
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 76 Of 250 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.