Whats 30 Percent Of 300
cibeltiagestion
Sep 11, 2025 · 5 min read
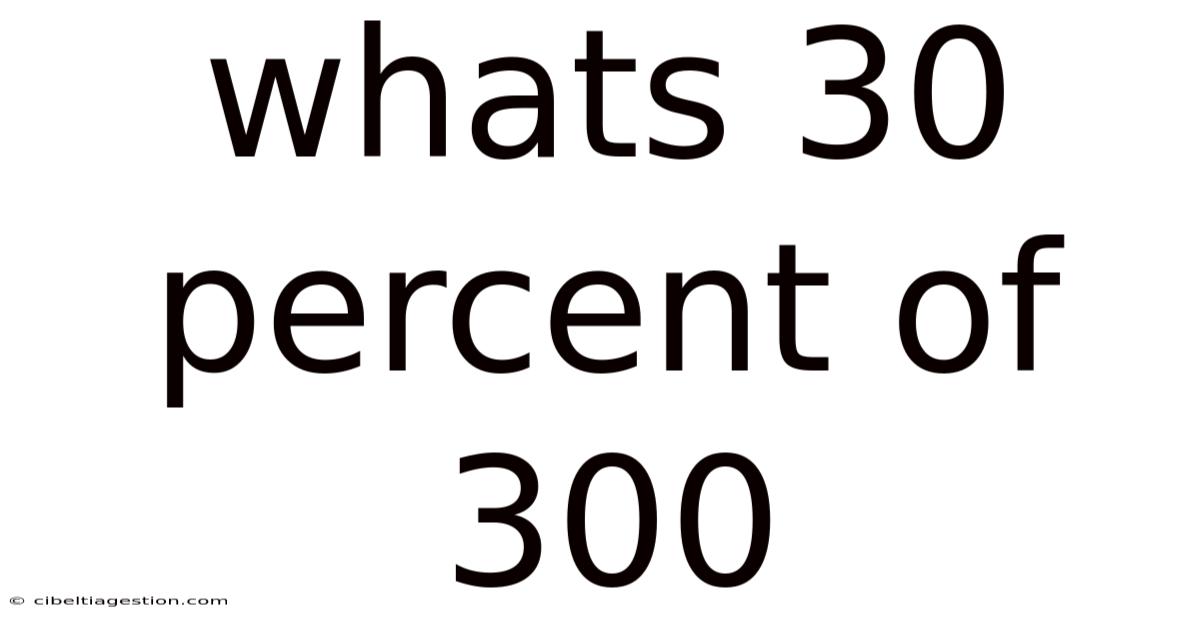
Table of Contents
What's 30 Percent of 300? A Deep Dive into Percentages and Their Applications
Finding 30 percent of 300 might seem like a simple task, easily solvable with a quick calculation. But this seemingly straightforward question opens the door to a broader understanding of percentages, their practical applications, and the underlying mathematical principles. This article will not only answer the question directly but will also delve into the methods of calculating percentages, exploring different approaches and demonstrating their usefulness in various real-world scenarios. We'll cover everything from basic arithmetic to more advanced percentage-based problems, ensuring you gain a comprehensive grasp of this fundamental mathematical concept.
Understanding Percentages: The Basics
Before tackling the specific problem of finding 30 percent of 300, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Understanding this fundamental concept is crucial because it allows us to convert between percentages, fractions, and decimals seamlessly. This flexibility is key to solving a wide range of percentage problems efficiently.
Method 1: Using the Decimal Equivalent
The most straightforward method for calculating 30 percent of 300 involves converting the percentage to its decimal equivalent. To do this, we divide the percentage by 100. In this case:
30% / 100 = 0.30
Now, we simply multiply this decimal by the original number:
0.30 * 300 = 90
Therefore, 30 percent of 300 is 90.
Method 2: Using the Fraction Equivalent
Alternatively, we can express 30% as a fraction:
30% = 30/100
This fraction can be simplified to 3/10. Now, we multiply this fraction by 300:
(3/10) * 300 = 90
Again, we arrive at the answer: 90. This method highlights the interchangeable nature of percentages, fractions, and decimals.
Method 3: The Proportion Method
The proportion method offers a more visual and intuitive approach to solving percentage problems. We can set up a proportion:
x / 300 = 30 / 100
Here, 'x' represents the unknown value (30% of 300). To solve for 'x', we cross-multiply:
100x = 30 * 300
100x = 9000
x = 9000 / 100
x = 90
This method reinforces the concept of proportional relationships and is particularly helpful for understanding the underlying logic of percentage calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world situations. Here are a few examples:
- Sales and Discounts: Calculating discounts offered during sales events. For example, a 20% discount on a $500 item.
- Taxes and Interest: Determining the amount of sales tax or interest payable on loans or investments.
- Statistics and Data Analysis: Representing data proportions and changes over time using percentages. For instance, understanding population growth or market share changes.
- Financial Planning: Calculating budgets, investment returns, and financial projections.
- Scientific Research: Expressing experimental results and uncertainties as percentages.
- Everyday Life: Tip calculations in restaurants, figuring out sale prices, understanding nutrition labels (percentage of daily value).
Beyond the Basics: More Complex Percentage Problems
While finding 30 percent of 300 is a relatively simple calculation, the principles can be extended to solve more complex problems. Consider these examples:
- Finding the original value: If a discounted item costs $70 after a 30% discount, what was the original price?
To solve this, we can set up an equation:
Original Price * (1 - 0.30) = $70
Original Price * 0.70 = $70
Original Price = $70 / 0.70 = $100
The original price was $100.
- Calculating percentage increase or decrease: If a quantity increases from 200 to 250, what is the percentage increase?
First, calculate the difference: 250 - 200 = 50
Then, divide the difference by the original value and multiply by 100:
(50 / 200) * 100 = 25%
The percentage increase is 25%.
- Percentage of a percentage: What is 20% of 15% of 1000?
First, calculate 15% of 1000: 0.15 * 1000 = 150
Then, calculate 20% of 150: 0.20 * 150 = 30
The answer is 30.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include: Incorrectly converting percentages to decimals, forgetting to multiply or divide by 100, and misinterpreting percentage increases or decreases. Carefully reviewing the steps involved and double-checking calculations can help avoid errors.
Q: Are there any shortcuts for calculating percentages mentally?
A: For certain percentages like 10%, 25%, and 50%, mental shortcuts are possible. 10% is simply moving the decimal point one place to the left. 25% is equivalent to one-quarter, and 50% is one-half. Practice with these simpler percentages can build mental agility for more complex calculations.
Q: What are some tools or resources available for calculating percentages?
A: Besides the standard calculator, numerous online percentage calculators and spreadsheet software (like Microsoft Excel or Google Sheets) offer convenient ways to calculate percentages efficiently.
Q: How can I improve my understanding and skills in working with percentages?
A: Consistent practice is key. Start with simple problems and gradually work towards more challenging ones. Utilize different calculation methods to build a deeper understanding and choose the method that best suits your individual learning style.
Conclusion
Finding 30 percent of 300 – which is 90 – is a stepping stone to a much broader understanding of percentages. This seemingly simple calculation unlocks a world of practical applications across various disciplines. By mastering the different methods for calculating percentages – using decimal equivalents, fractions, and the proportion method – you equip yourself with a valuable skill applicable to numerous real-world situations. Remember, consistent practice and understanding the underlying principles are crucial for developing proficiency in working with percentages effectively. Whether you’re calculating discounts, analyzing data, or managing finances, a solid grasp of percentage calculations empowers you to make informed decisions and navigate numerical challenges confidently.
Latest Posts
Latest Posts
-
Stereotypical Behaviors Sometimes Include Objects
Sep 12, 2025
-
What Is A Pilgrimage Church
Sep 12, 2025
-
Computer Parts You Can Touch
Sep 12, 2025
-
4 Ft 3 In Inches
Sep 12, 2025
-
What Is 75 Of 27
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 30 Percent Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.