X 2 5x 14 0
cibeltiagestion
Sep 02, 2025 · 5 min read
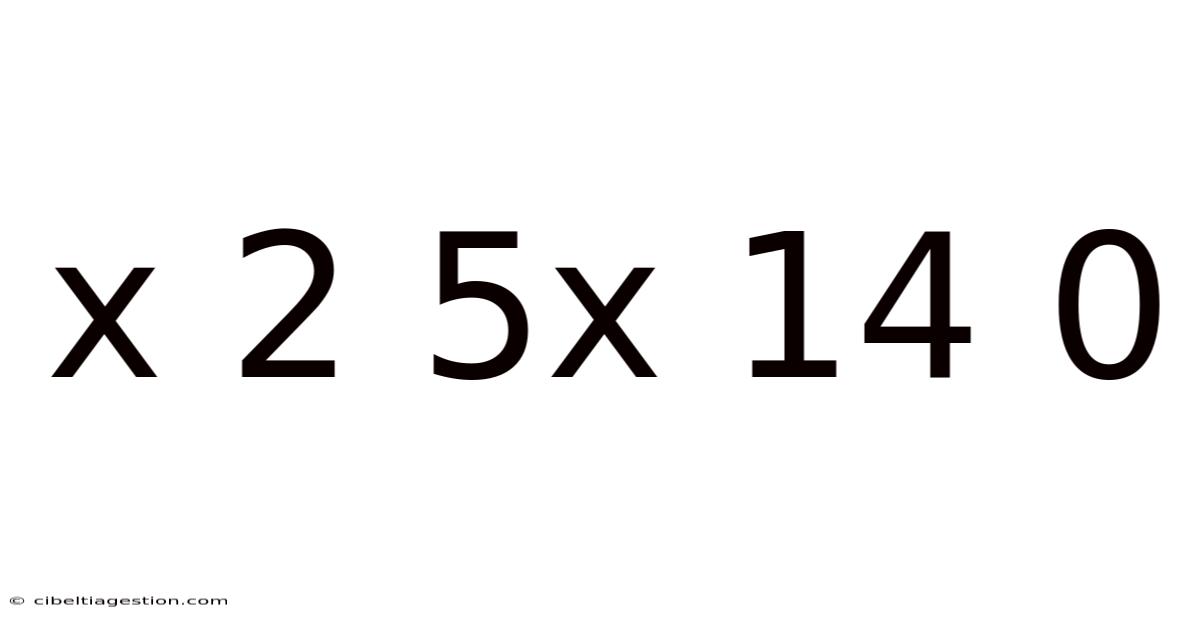
Table of Contents
Decoding the Sequence: x 2 5x 14 0 - A Deep Dive into Pattern Recognition and Mathematical Reasoning
This article explores the mathematical sequence "x 2 5x 14 0," delving into various approaches to understanding the pattern, identifying potential solutions for 'x', and discussing the broader mathematical concepts involved. We'll move beyond a simple answer to explore the underlying principles of pattern recognition and problem-solving, making this a valuable resource for students and anyone interested in mathematical reasoning.
Introduction: Unveiling the Mystery
The sequence "x 2 5x 14 0" presents a fascinating challenge. At first glance, it seems cryptic. However, by applying logical reasoning and mathematical techniques, we can unravel the hidden pattern and potentially determine the value of 'x'. This seemingly simple sequence allows us to explore concepts like algebraic manipulation, quadratic equations, and the importance of context in mathematical problem-solving. The core of this exploration lies in identifying the relationships between the numbers and leveraging those relationships to find a solution.
Understanding the Nature of the Problem
Before jumping into solutions, it's crucial to define the problem. We're dealing with a sequence of numbers where 'x' represents an unknown variable. The sequence suggests a relationship exists between these numbers. Our task is to discover this relationship and find the value(s) of 'x' that satisfy the pattern. The absence of explicit operators between the numbers initially makes the problem more challenging, prompting us to consider different interpretations and possibilities.
Possible Interpretations and Approaches
The ambiguity of the sequence allows for multiple interpretations, each leading to different approaches:
-
Arithmetic Progression (unlikely): An arithmetic progression involves a constant difference between consecutive terms. This is highly unlikely given the presence of 'x' and the disparate nature of the numbers.
-
Geometric Progression (unlikely): A geometric progression involves a constant ratio between consecutive terms. Again, the presence of 'x' and the lack of an obvious ratio make this interpretation improbable.
-
Polynomial Relationship: This is the most likely approach. The sequence could represent a polynomial function where the terms are the results of substituting consecutive integers into the equation. This approach will be explored in detail.
-
Hidden Operations: We might need to consider that the numbers represent results of an operation using an unknown function. The function needs to explain the observed relationships among the given values in the sequence.
Solving Using a Polynomial Approach
Let's assume the sequence represents a polynomial function. Given four terms (including 'x'), we can assume at most a cubic polynomial, represented by:
f(n) = an³ + bn² + cn + d
where 'n' is the term's position in the sequence (1, 2, 3, 4).
We can now use the given sequence to set up a system of equations:
- f(1) = x
- f(2) = 2
- f(3) = 5x
- f(4) = 140
This yields four equations with four unknowns (a, b, c, and d):
- a + b + c + d = x
- 8a + 4b + 2c + d = 2
- 27a + 9b + 3c + d = 5x
- 64a + 16b + 4c + d = 140
Solving this system of equations simultaneously is complex and requires advanced algebraic techniques. It's highly probable that simpler relationships might exist, possibly involving a quadratic equation or other less complex functions, but exploration of the cubic option provides a rigorous mathematical process. We may also find that a specific solution doesn't exist within a realistic framework based on whole numbers and common arithmetic operations.
Exploring Simpler Relationships: Quadratic Equations
A more pragmatic approach is to explore the possibility of a quadratic relationship. This approach is chosen since it offers a higher probability for a clean mathematical solution. We can attempt to fit a quadratic equation of the form:
f(n) = an² + bn + c
This approach requires us to make assumptions or introduce additional constraints to solve for the unknowns. For example, we might assume that the sequence represents some form of pattern that holds some significance even if we cannot directly solve for 'x' through the standard means of solving a cubic or quadratic equation.
For instance, we might consider the differences between consecutive terms to find some regularity. A key concept is to systematically assess how the differences, or second differences between the terms, may help identify patterns. This methodical approach offers a more explorative approach.
Advanced Techniques: Interpolation and Extrapolation
To address the complexity of solving the system of equations, advanced techniques like Lagrange interpolation could be applied. Lagrange interpolation is a method for finding a polynomial that passes through a given set of points. While this method can provide a solution, it doesn't necessarily guarantee that the resulting polynomial reflects the underlying pattern intended by the problem, particularly if there are other possible interpretations of the sequence.
Furthermore, extrapolation can be used to estimate the values beyond the given sequence. However, the accuracy of extrapolation depends heavily on the accuracy of the underlying model. The method is prone to large errors when we try to extrapolate far beyond the known data points.
The Importance of Context and Additional Information
The difficulty in solving for 'x' definitively highlights the importance of context in mathematical problems. The sequence "x 2 5x 14 0" is incomplete without additional information or constraints. It's possible this sequence is part of a larger problem, or there might be unspoken rules or relationships governing the numbers.
Conclusion: A Journey into Mathematical Reasoning
The sequence "x 2 5x 14 0" serves as an excellent example of how mathematical problems can require creativity, multiple approaches, and a thorough understanding of underlying principles. While a definitive solution for 'x' might be elusive without further context, the process of exploring different interpretations and applying various mathematical techniques is invaluable. The exploration of different methods, such as assessing whether a linear, quadratic or even cubic polynomial relation applies, expands our problem-solving tool kit. It also underlines the significance of recognizing patterns and utilizing diverse strategies in approaching mathematical challenges. The exercise emphasizes that mathematical problem-solving is not merely about finding answers but about cultivating the ability to think critically, reason logically, and appreciate the beauty and complexity of mathematical relationships. The journey of exploring this sequence offers a valuable lesson in mathematical thinking, far beyond just arriving at a numerical solution for 'x'. This journey enhances our ability to analyze complex situations and approach problem-solving methodically, a skill vital not just in mathematics but in many aspects of life.
Latest Posts
Latest Posts
-
What Is 20 Of 2500
Sep 02, 2025
-
5 Foot 7 To Cm
Sep 02, 2025
-
Which Phrase Defines Complementary Goods
Sep 02, 2025
-
Half Of 2 1 2
Sep 02, 2025
-
Free Mastering Biology Access Code
Sep 02, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 14 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.