5n 34 2 1 7n
cibeltiagestion
Sep 10, 2025 · 5 min read
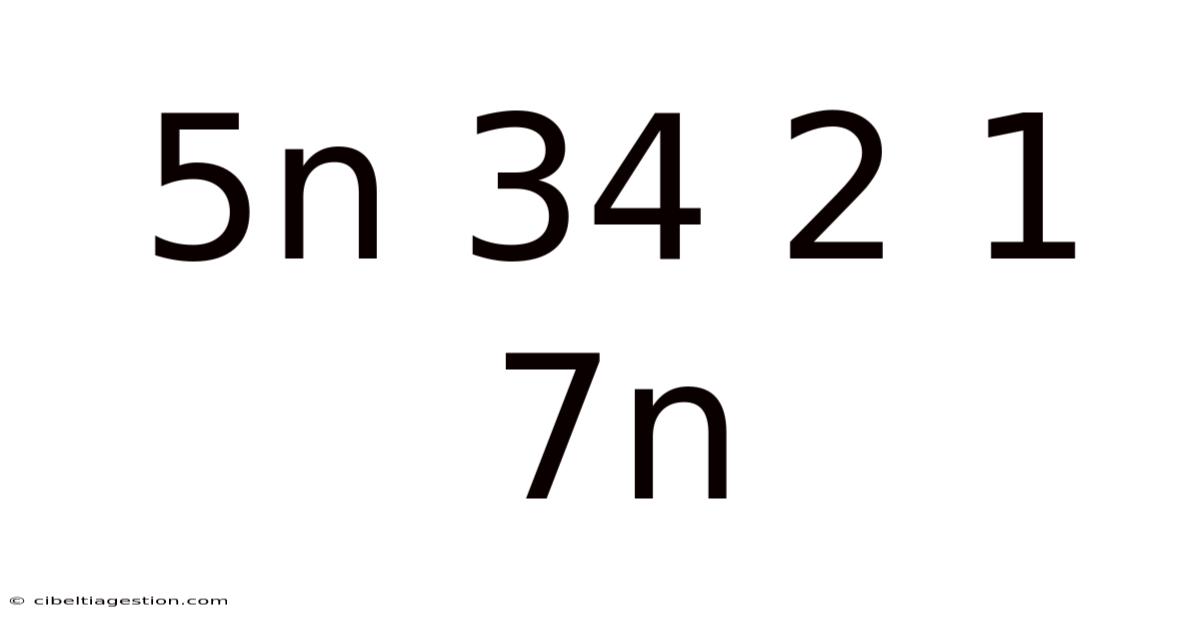
Table of Contents
Decoding the Enigma: An In-Depth Exploration of the Sequence 5n 34 2 1 7n
The seemingly random sequence "5n 34 2 1 7n" presents a fascinating challenge. At first glance, it appears to be a meaningless collection of numbers and symbols. However, a deeper dive reveals potential mathematical relationships, logical patterns, and even possibilities for coding or cryptography. This article will explore various interpretations of this sequence, aiming to uncover its hidden structure and potential meanings. We will delve into possible mathematical functions, explore potential coding schemes, and even consider the impact of context on interpretation. Ultimately, the goal is to transform this initially cryptic sequence into a comprehensible and engaging piece of intellectual exploration.
Understanding the Components: Numbers and Symbols
Before attempting to decipher the sequence, let's break down its individual components:
- Numbers: 5, 34, 2, 1, 7. These are integers, with no immediately obvious pattern or relationship. Their distribution appears arbitrary.
- Symbol 'n': The presence of 'n' strongly suggests the involvement of variables, typically used in algebraic expressions or programming. This implies the sequence might represent a formula or part of an algorithm.
The combination of numbers and a variable dramatically alters the scope of possible interpretations. It suggests that the sequence is not merely a sequence of numbers but potentially a mathematical expression or a fragment of a larger code.
Potential Mathematical Interpretations: Uncovering the Formula
The inclusion of 'n' strongly suggests a mathematical function is at play. Let's explore potential interpretations:
-
Simple Arithmetic Progressions: At first glance, the sequence doesn't follow a simple arithmetic progression (adding a constant value). However, we could consider variations or subsequences. For instance, are there any consistent differences between consecutive terms if we exclude 'n'?
-
Geometric Progressions: Similarly, a geometric progression (multiplying by a constant value) doesn't immediately present itself. However, more complex geometric relationships involving 'n' might exist.
-
Polynomial Functions: A more sophisticated approach would involve fitting the sequence to a polynomial function. Since we have five data points (assuming 'n' represents a specific value in each instance), we could potentially find a polynomial of degree four or less that fits the data. This would require solving a system of equations, which, while solvable, would be laborious and might not yield a meaningful result unless further context is provided.
-
Modular Arithmetic: It's possible the sequence represents operations within a specific modulus. Modular arithmetic deals with remainders after division. Exploring this avenue would involve testing different moduli to see if any consistent pattern emerges within the remainders.
-
Recursive Functions: The 'n' might suggest a recursive function, where each term is dependent on previous terms. This would require determining the recursive relationship between terms. The lack of readily apparent pattern makes this approach challenging without additional information.
Example of Polynomial Fitting (Illustrative): Let's assume 'n' represents the position of the number in the sequence (n=1, n=2, etc.). We could attempt to fit a polynomial to the points (1,5), (2,34), (3,2), (4,1), (5,7). This process involves solving a system of linear equations, which may or may not provide a meaningful or insightful polynomial.
Potential Coding or Cryptographic Interpretations: Beyond Mathematics
The sequence could represent a code or a fragment of a cipher. Several possibilities exist:
-
Substitution Cipher: Each number could represent a letter or symbol based on a substitution key. Without a key, deciphering this is impossible.
-
Affine Cipher: An affine cipher involves a linear transformation of the input. This could be relevant if 'n' represents an input value transformed by the sequence.
-
Vigenère Cipher: This is a polyalphabetic substitution cipher using a keyword. If the sequence represents a key or part of a key for this cipher, further information would be necessary to decipher any message encrypted with it.
-
Binary Code: The numbers could be converted to their binary equivalents. This might reveal a pattern or message when the binary representations are concatenated or analyzed in a specific manner. For example, 5 in binary is 101, 34 is 100010, etc.
The Importance of Context: Unlocking the Sequence's True Meaning
Crucially, the interpretation of the sequence greatly depends on the context in which it appears. The meaning of "5n 34 2 1 7n" could radically change depending on:
-
Source: Where did the sequence come from? A mathematical textbook? A programming code snippet? A puzzle? A cryptographic message? The source provides vital clues.
-
Surrounding Information: What other information is available alongside the sequence? Are there instructions? A description? Related equations or data? All of these could significantly aid in understanding the sequence.
-
Intended Audience: Who is the intended recipient or interpreter of the sequence? This influences the complexity of the interpretation. A simple sequence for a child will differ from a complex code for a cryptographer.
Frequently Asked Questions (FAQ)
-
Q: Is there a single definitive answer to the meaning of this sequence?
A: No. Without additional context, there isn't a single, definitive interpretation. Multiple mathematical and coding possibilities exist.
-
Q: Can I use this sequence in a mathematical model?
A: Potentially, yes. If the sequence is a fragment of a larger formula or algorithm, incorporating it into a broader model might be possible, but only if you understand the underlying function.
-
Q: How can I approach deciphering similar sequences?
A: Start by analyzing the components (numbers, symbols). Look for patterns (arithmetic, geometric, modular). Consider possible mathematical functions (polynomials, recursive functions). Explore coding possibilities (substitution, affine, Vigenère). Most importantly, determine the context in which the sequence appears.
-
Q: What if the sequence represents a real-world phenomenon?
A: This is a possibility, although less likely without further context. The sequence could represent data points from a physical process, but understanding what that process is would require additional information.
Conclusion: A Journey of Exploration
The sequence "5n 34 2 1 7n" serves as a fascinating illustration of how seemingly random data can hold hidden meaning. Unraveling its secrets requires a systematic approach, exploring mathematical functions, coding possibilities, and, most critically, seeking further context. This exploration highlights the importance of understanding the surrounding information to interpret cryptic data correctly. Without more context, the sequence remains enigmatic, providing a tantalizing challenge for those who enjoy the thrill of solving puzzles and deciphering codes. The lack of a single, definitive answer underscores the beauty and complexity of such open-ended problems, encouraging further investigation and creative problem-solving. The journey of deciphering this sequence underscores the intellectual curiosity and deductive reasoning necessary to uncover hidden patterns and knowledge within seemingly random data sets.
Latest Posts
Latest Posts
-
77 200 In Decimal Form
Sep 10, 2025
-
Four Legs In The Morning
Sep 10, 2025
-
Factor 2x 2 7x 3
Sep 10, 2025
-
What Is 76 Of 250
Sep 10, 2025
-
Evaluate 32 2 6 10
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 5n 34 2 1 7n . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.