Square Root Of 2x Squared
cibeltiagestion
Sep 10, 2025 · 6 min read
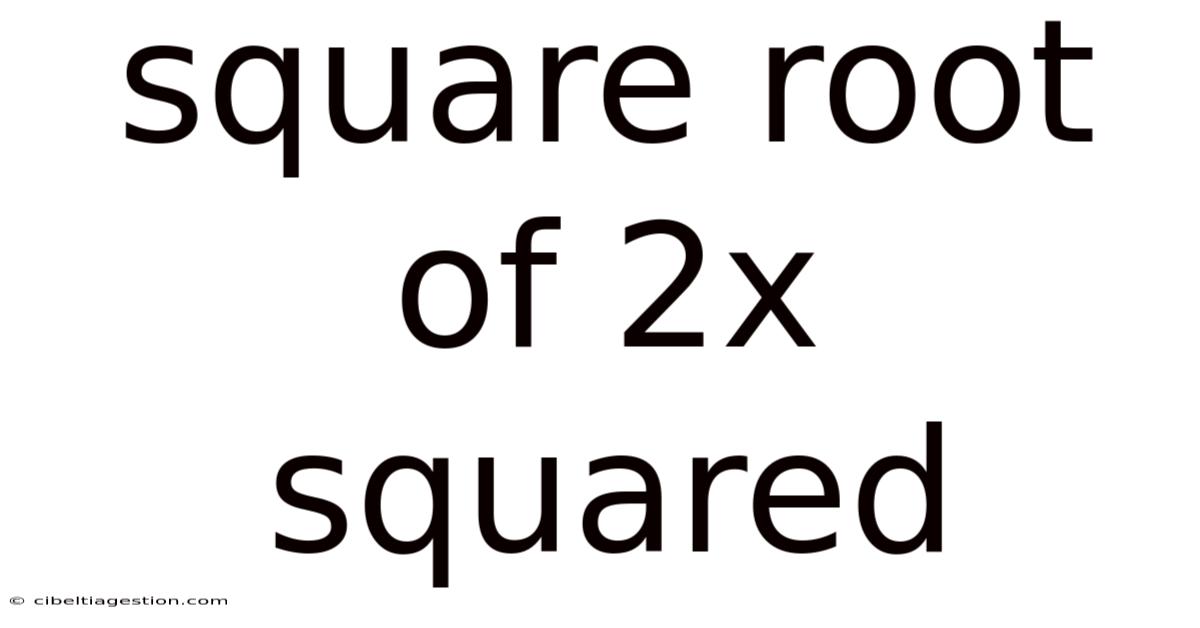
Table of Contents
Understanding the Square Root of 2x²: A Comprehensive Guide
The square root of 2x², often encountered in algebra and calculus, might seem daunting at first glance. However, with a structured approach and a clear understanding of fundamental mathematical principles, this seemingly complex concept becomes easily manageable. This comprehensive guide will break down the process of simplifying and understanding the square root of 2x², exploring its properties, applications, and potential pitfalls. We'll delve into the nuances of simplifying radicals, covering both positive and negative solutions, and examining how this concept relates to more advanced mathematical concepts.
Introduction: Deconstructing the Problem
The expression √(2x²) represents the principal square root of 2x². The term "principal square root" refers to the non-negative root. Understanding this is crucial because the square root of a number can have both a positive and a negative solution (e.g., √9 = ±3). However, the principal square root function, denoted by the radical symbol (√), always returns the non-negative value. Our exploration will cover both scenarios, ensuring a thorough understanding.
The key to simplifying √(2x²) lies in understanding the properties of radicals and how they interact with coefficients and variables. We'll utilize the following crucial properties throughout this guide:
- √(ab) = √a * √b: The square root of a product is the product of the square roots.
- √(a/b) = √a / √b: The square root of a quotient is the quotient of the square roots.
- √(a²) = |a|: The square root of a squared number is the absolute value of that number. This ensures the result is always non-negative.
Simplifying √(2x²) Step-by-Step
Let's break down the simplification process systematically:
-
Separate the terms: We can rewrite √(2x²) as √2 * √(x²). This utilizes the property √(ab) = √a * √b.
-
Simplify √(x²): The square root of x² is |x|. Remember, the result must be non-negative, hence the use of absolute value. This stems from the property √(a²) = |a|.
-
Combine the simplified terms: This gives us |x|√2.
Therefore, the simplified form of √(2x²) is |x|√2.
Understanding the Absolute Value
The inclusion of the absolute value, |x|, is crucial. It guarantees that the final result is always non-negative, adhering to the definition of the principal square root. If we were to consider all possible solutions (both positive and negative), the expression would be ±x√2. However, when specifically dealing with the principal square root, the absolute value ensures the correct non-negative solution.
For example:
- If x = 2, then √(2x²) = √(2 * 2²) = √8 = 2√2. This aligns with |x|√2 = |2|√2 = 2√2.
- If x = -2, then √(2x²) = √(2 * (-2)²) = √8 = 2√2. This also aligns with |x|√2 = |-2|√2 = 2√2.
This highlights the importance of the absolute value in ensuring the correct principal square root is always obtained, regardless of the sign of x.
Expanding the Concept: Considering Different Scenarios
While the simplified form |x|√2 provides the principal square root, it's beneficial to explore scenarios where the context alters our approach:
Scenario 1: Restricting the Domain
If the problem explicitly states that x is non-negative (x ≥ 0), then the absolute value becomes redundant, and the simplified expression reduces to x√2. This simplification is valid only under this specific condition.
Scenario 2: Solving Equations
When solving equations involving √(2x²), we must remember that both positive and negative solutions are possible. For instance, if we have the equation √(2x²) = 4, we would solve as follows:
- |x|√2 = 4
- |x| = 4/√2
- |x| = 2√2
- Therefore, x = ±2√2
Here, both positive and negative solutions are valid because we're not explicitly dealing with the principal square root function alone.
Scenario 3: Complex Numbers
If x were a complex number (involving the imaginary unit 'i'), the simplification would remain the same, although the interpretation of absolute value would need to be extended to the complex plane (using the magnitude of the complex number).
The Scientific Rationale: Why Absolute Value is Essential
The importance of the absolute value function in the simplification of √(2x²) is deeply rooted in the fundamental properties of square roots and real numbers. The square root operation is defined to return only non-negative values. This is a crucial aspect of mathematical consistency, preventing ambiguities and ensuring that functions remain well-defined. The absolute value function precisely enforces this non-negativity, ensuring that regardless of the input value of x (positive or negative), the output of √(2x²) remains non-negative. Without the absolute value, the output would be ambiguous and potentially contradictory to the definition of the square root operation.
Applications in Various Fields
The simplification of expressions like √(2x²) finds applications in various fields:
-
Physics: Calculations involving distance, velocity, and acceleration often involve square roots. For example, calculating the magnitude of a vector in two dimensions might involve such an expression.
-
Engineering: Design and analysis in structural engineering frequently uses square roots in calculations related to forces, stresses, and strains.
-
Computer Graphics: In algorithms for 2D or 3D graphics rendering, these types of expressions can be found in calculations involving distances between points or transformations.
-
Economics and Finance: Financial modeling may use these calculations in areas involving standard deviation or other statistical measures.
Frequently Asked Questions (FAQ)
Q1: Can I simply write √(2x²) as x√2?
A1: No, not without specifying that x ≥ 0. Writing √(2x²) as x√2 implies that x is always non-negative, which is not true in general. The correct simplification, encompassing all real values of x, is |x|√2.
Q2: What if x is zero?
A2: If x = 0, then √(2x²) = √(2 * 0²) = √0 = 0. This aligns with both |x|√2 and x√2 when x = 0.
Q3: How does this relate to more advanced mathematical concepts?
A3: The concepts involved in simplifying this expression lay the groundwork for understanding more complex topics such as:
- Calculus: Differentiating and integrating expressions involving radicals is built upon the fundamental principles of simplifying radicals.
- Linear Algebra: Understanding the properties of vectors and matrices often relies on concepts related to magnitudes and norms, which frequently involve square roots.
- Complex Analysis: Extending the concept to complex numbers requires a deeper understanding of complex numbers and their magnitudes.
Conclusion: Mastering the Fundamentals
Simplifying √(2x²) might seem like a small detail in the vast landscape of mathematics, but it's a fundamental concept that highlights important aspects of algebra and the handling of radicals. Mastering this concept strengthens your understanding of square roots, absolute values, and the importance of mathematical precision. Remember, the correct and universally applicable simplified form is |x|√2, emphasizing the crucial role of the absolute value in ensuring the non-negativity of the principal square root, regardless of the sign of x. Understanding the nuances of absolute value in this context will be invaluable as you delve deeper into more complex mathematical explorations.
Latest Posts
Latest Posts
-
Wingdings Font Character Code 110
Sep 10, 2025
-
1 8 Divided 3 4
Sep 10, 2025
-
4 5 Million Yen To Usd
Sep 10, 2025
-
5 2 Independent Practice Answer Key
Sep 10, 2025
-
C3h5 No3 3 Molar Mass
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2x Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.