Y 3 Square Root X
cibeltiagestion
Sep 01, 2025 · 7 min read
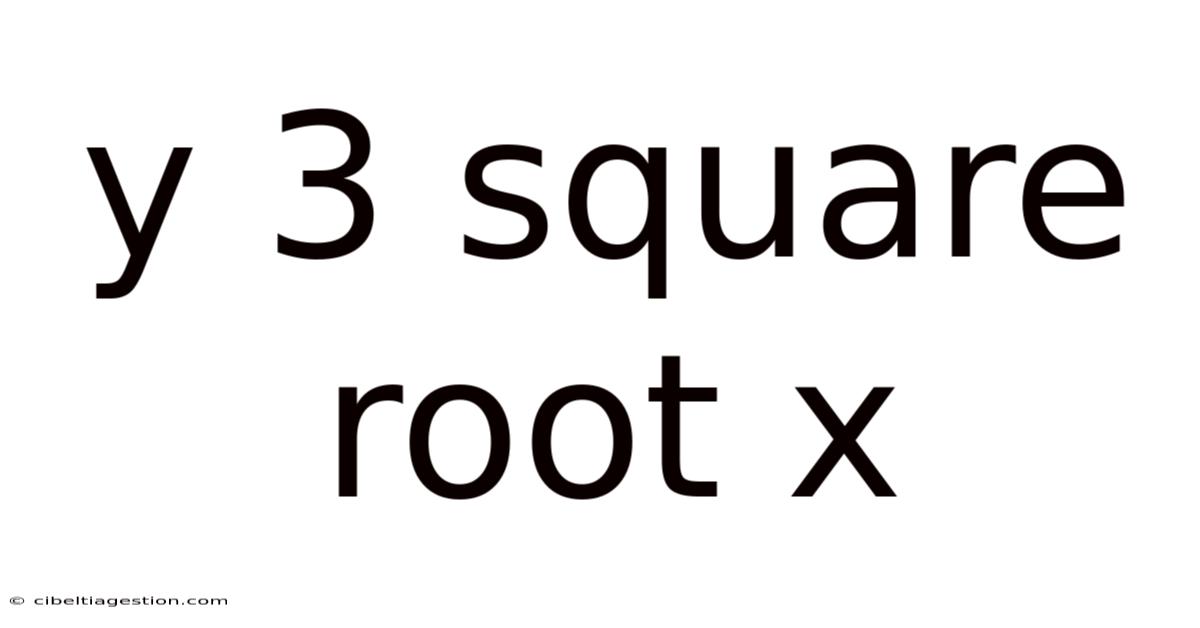
Table of Contents
Unveiling the Mysteries of y = 3√x: A Comprehensive Exploration
The equation y = 3√x, or equivalently y = x^(1/3), represents a fundamental concept in mathematics, specifically within the realm of radical functions and power functions. Understanding its properties, graph, and applications is crucial for a strong foundation in algebra, calculus, and beyond. This article will delve into a comprehensive exploration of y = 3√x, covering its characteristics, derivations, applications, and frequently asked questions. We'll move beyond simple calculations to uncover the deeper mathematical significance of this seemingly straightforward equation.
Introduction: Understanding the Cube Root Function
The expression 3√x denotes the cube root of x. This means finding a number that, when multiplied by itself three times, results in x. For example, 3√8 = 2 because 2 * 2 * 2 = 8. Unlike the square root, which is only defined for non-negative numbers, the cube root is defined for all real numbers, both positive and negative. This is because a negative number multiplied by itself three times yields a negative result. For instance, 3√-8 = -2 because (-2) * (-2) * (-2) = -8. The equation y = 3√x demonstrates this function graphically, showing the relationship between x and its cube root.
Graphing y = 3√x: Visualizing the Function
The graph of y = 3√x is a smooth, continuous curve that extends infinitely in both the positive and negative x and y directions. Key characteristics of the graph include:
- Origin: The curve passes through the origin (0, 0) because the cube root of 0 is 0.
- Symmetry: The graph exhibits odd symmetry, meaning it is symmetric about the origin. This means that if (a, b) is a point on the graph, then (-a, -b) is also a point on the graph. This reflects the property that the cube root of a negative number is the negative of the cube root of its positive counterpart.
- Increasing Function: The function is strictly increasing. As x increases, y also increases. This means the graph continuously rises from left to right.
- Asymptotes: The function does not have any vertical or horizontal asymptotes. It extends infinitely in all directions.
- Concavity: The graph is concave down for x > 0 and concave up for x < 0. The point of inflection occurs at the origin (0,0).
Understanding the shape of the graph provides crucial insight into the behavior of the cube root function and helps in solving related problems. Sketching the graph, even a rudimentary one, allows you to visualize the relationship between the input (x) and the output (y).
Mathematical Properties and Derivations
Let's delve deeper into the mathematical properties of y = 3√x:
- Power Function Representation: The cube root function can be written as a power function: y = x^(1/3). This representation is useful in calculus, allowing us to apply power rule for differentiation and integration.
- Inverse Function: The inverse function of y = x³ is y = 3√x. This means that if you cube a number and then take the cube root of the result, you obtain the original number. Similarly, taking the cube root of a number and then cubing the result gives the original number.
- Differentiation: Using the power rule of differentiation, the derivative of y = x^(1/3) is dy/dx = (1/3)x^(-2/3). This derivative represents the slope of the tangent line at any point on the graph. Note that the derivative is undefined at x = 0, which corresponds to the point of inflection.
- Integration: The indefinite integral of y = x^(1/3) is ∫x^(1/3)dx = (3/4)x^(4/3) + C, where C is the constant of integration. This integral represents the area under the curve.
Real-World Applications of the Cube Root Function
While the cube root function might seem abstract, it finds applications in diverse fields:
- Physics: Cube roots frequently appear in physics problems related to volume and scaling. For example, if you double the length of the sides of a cube, its volume increases eightfold (2³). Conversely, finding the side length given the volume involves taking the cube root.
- Engineering: Similar to physics, engineering problems involving volume calculations, fluid dynamics, or scaling often necessitate the use of cube roots.
- Statistics: In statistical analysis, particularly in data distributions, the cube root can be used to stabilize variance or transform data for better analysis.
- Geometry: The cube root appears in calculations involving volumes of cubes, spheres, and other three-dimensional shapes.
- Biology: Certain biological growth models can be described using cube root functions.
Solving Equations Involving Cube Roots
Solving equations involving cube roots often involves algebraic manipulation. The key is to isolate the cube root term and then cube both sides of the equation to eliminate the radical. For example, to solve the equation 3√(x + 2) = 4, we follow these steps:
- Isolate the cube root: The equation is already isolated.
- Cube both sides: (3√(x + 2))³ = 4³ This simplifies to x + 2 = 64.
- Solve for x: x = 64 - 2 = 62.
Always check your solution by substituting it back into the original equation to ensure it's correct.
Advanced Concepts and Extensions
For those seeking a deeper understanding, we can explore more advanced aspects of the cube root function:
- Complex Numbers: The cube root function can be extended to complex numbers. A complex number has a real and an imaginary part. Finding the cube root of a complex number involves finding three distinct solutions in the complex plane.
- Series Expansions: The cube root function can be represented by an infinite power series, particularly useful in numerical analysis and approximations.
- Numerical Methods: For finding cube roots of numbers that aren't easily calculable manually, numerical methods such as the Newton-Raphson method provide efficient approximations.
Frequently Asked Questions (FAQ)
Q1: What is the difference between the cube root and the square root?
A1: The square root of a number x (√x) is a number that, when multiplied by itself, equals x. The cube root of a number x (3√x) is a number that, when multiplied by itself three times, equals x. The square root is only defined for non-negative numbers, while the cube root is defined for all real numbers.
Q2: Can the cube root of a number be negative?
A2: Yes, the cube root of a negative number is negative. For example, 3√-27 = -3 because (-3) * (-3) * (-3) = -27.
Q3: How do I calculate the cube root of a number without a calculator?
A3: For perfect cubes, you can determine the cube root by recognizing the number as the cube of an integer. For other numbers, it’s difficult to calculate precisely without a calculator or numerical methods. Approximation techniques can be used, but they usually require iterative processes.
Q4: What are some common mistakes when working with cube roots?
A4: Common mistakes include forgetting that the cube root of a negative number is negative, incorrectly applying the rules of exponents, and making algebraic errors while solving equations involving cube roots.
Q5: Is the cube root function continuous?
A5: Yes, the cube root function, y = x^(1/3), is continuous for all real numbers. There are no breaks or discontinuities in its graph.
Conclusion: A Deeper Appreciation of y = 3√x
This comprehensive exploration has illuminated the multifaceted nature of the equation y = 3√x. From its graphical representation and mathematical properties to its applications in various fields, we've uncovered the significance of this seemingly simple function. Understanding the cube root function is not just about memorizing formulas; it's about grasping its underlying principles and appreciating its role in the broader landscape of mathematics and its real-world applications. By exploring its intricacies, we gain a more profound understanding of the power and elegance of mathematical concepts. Further exploration into its advanced aspects, such as complex number analysis and numerical methods, will reveal even more of its richness and potential.
Latest Posts
Latest Posts
-
Why Are Financial Values Important
Sep 01, 2025
-
Is Pcl5 Polar Or Nonpolar
Sep 01, 2025
-
0 1 X 0 2 X 2
Sep 01, 2025
-
Which Statement Is True About
Sep 01, 2025
-
What Is 10 Of 35
Sep 01, 2025
Related Post
Thank you for visiting our website which covers about Y 3 Square Root X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.